これは AfterEffects Advent Calendar 2016 の2日目の記事です。昨日はむらしんさんで、レイヤーにモテモテ、カメラテクニックでした。お疲れ様でした。
ところで皆さん、AE、使ってますか?
AEは素晴らしいツールです。使っていないという方は今すぐAdobeと契約してAEerになってよ! /人◕‿‿◕人\
ところで皆さん、イージング、使ってますか?
イージングが何っていう人は「【AEオフ2016】キーフレームとグラフエディタ(甘)」とかを見るといいんじゃないでしょうか。
とりあえず、影響度100%だけ覚えて帰って頂ければ幸いです。ご清聴ありがとうございました。
ところで皆さん、エクスプレッション、使ってますか?
エクスプレッションでイージングを行うというのは、キーフレームやEase and Wizzなどと比べてめんどくさいという説もあるのですが、様々な動きを実現することができるため、自分はよく使用しています。
特に使っているのが指数関数で、非常に鋭い動きをすることで有名です。
ですが、この完全無欠に見える指数関数でも不満がないわけではありません。それを感じる状況のひとつは、減衰が強すぎると感じる場合です。特に、少し長いカットでは、減衰後の停止が気になってしまうかもしれません。しかしながら、指数関数の係数を小さくしてイージングの速度を遅くすると、今度は動きにメリハリが無くなってしまい、優しさに溢れた動きにはなるのですが、少しかっこ悪くなってしまいます。(なんかこういろいろかっこいいパーティクルとか使ってバーってやれば良いような気もしますが、それはおいといて・・・)
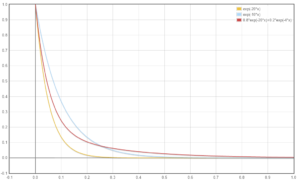
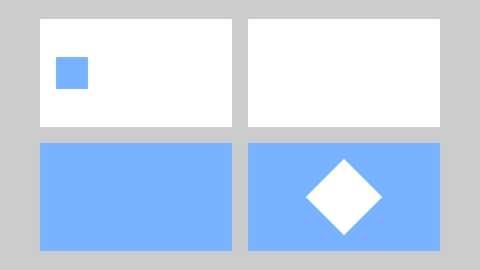
そこで、指数関数を2つ加えれば良いんじゃない!? となります。その映像がこちらになります。
左の列から順に、キーフレーム(影響度100%)、指数関数(係数20)、指数関数(係数10)、混合指数関数となっています。
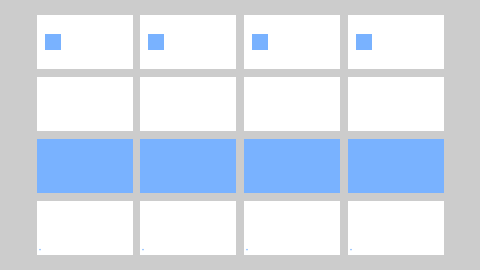
$$ f_2(t) = e^{-20t}$$
$$ f_3(t) = e^{-10t}$$
$$ f_4(t) = 0.8 e^{-20t} + 0.2 e^{-4t}$$
グラフにすると以下のようになります。
途中で大小関係が逆転しているのがわかります。
使用例
どこがキーフレームでどこが指数でどこが混合指数だったかは忘れましたが、これらがの関数が使い分けて使用されています。
このように、2つ(以上)の指数関数を組み合わせることで、より艶めかしい動きを作ることができます。多分。皆さんも是非試してみてください。
と、これで言いたかった話は終わりなのですが、記事が短いと思ったのでもう少しだけ話を続けてみたいと思います。
この新しいイージング関数に対して思うのは、「減衰が強すぎるのが嫌なら多項式関数とかで良いんじゃないの?」というものです。本当にこんな長いエクスプレッションを書かなければならないのでしょうか。他に似たようなことをできる簡単な関数はないのでしょうか。
この疑問を自己解決すべく、何種類かの関数をグラフにしてみました。
条件
比較をしやすくするために、次のような条件を付けましょう。
$$ f(0) = 1 $$
$$ f(\infty) = 0 $$
$$ f'(0) = -20 $$
$$ f(t) $$ は単調減少である
この条件に従うと、先程の混合指数関数は次のように表せます。
$$ f_5(t) = 0.8 e^{-20t/0.84} + 0.2 e^{-4t/0.84} $$
では行ってみましょう。
$$x<0$$の一点で極を持つ有理関数(多項式関数の逆数)
一般式が $$ f(x) = 1/(ax+b)^c $$ であるとします。これを上の条件に従って解くと、 $$ b=1, ac=20 $$ が導かれるため、この式は $$ f(x) = 1/(ax+1)^{20/a} $$ と書き換えることができます。この場合はどうなるでしょうか。
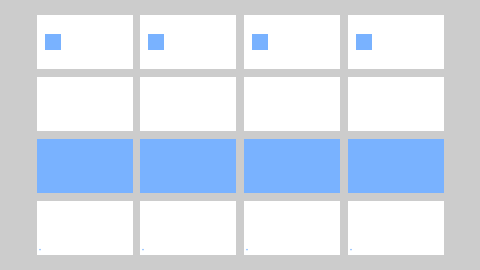
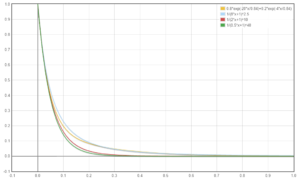
左から順に、次のようになっています。
$$ f_5(t) = 0.8 e^{-20t/0.84} + 0.2 e^{-4t/0.84} $$
$$ f_6(t) = 1/(8t+1)^{2.5}$$
$$ f_7(t) = 1/(2t+1)^{10}$$
$$ f_8(t) = 1/(0.5t+1)^{40}$$
グラフにすると以下のようになります。
完全に同じではありませんが、a=8のもの(左から2番目)などは、一番左のものに近い形になったのではないでしょうか?
多項式関数
一般式が $$ f(x) = |ax-b|^c $$ であるとします。これを上の条件に従って解くと、 $$ b=1, ac=20 $$ が導かれるため、この式は $$ f(x) = |ax-1|^{20/a} $$ と書き換えることができます。ただし、単調減少である必要があるので、$$ \{\mathrm{max}(1-ax, 0)\}^{20/a} $$ とします。この場合はどうなるでしょうか。
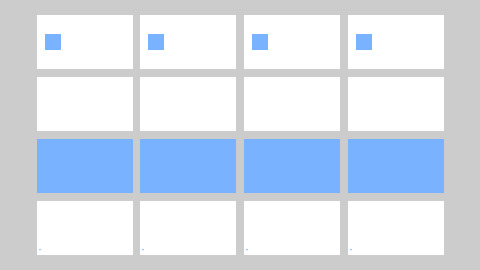
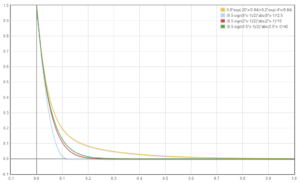
左から順に、次のようになっています。
$$ f_5(t) = 0.8 e^{-20t/0.84} + 0.2 e^{-4t/0.84} $$
$$ f_9(t) = \{\mathrm{max}(1-8x, 0)\}^{2.5}$$
$$ f_{10}(t) = \{\mathrm{max}(1-2x, 0)\}^{10}$$
$$ f_{11}(t) = \{\mathrm{max}(1-0.5x, 0)\}^{40}$$
グラフにすると以下のようになります。
このように、あまりいい感じにはなりませんでした。
他にも試してみたい関数はありますが、力尽きてしまったのでここまでとなります。全く解析学の要素がありませんでしたが、いかがでしたか? つまらない記事にお付き合い頂き本当にありがとうございました。
もっと良いエクスプレッションがあるよ、とか、スクリプトで解決できるよ、みたいな話がありましたらTwitterや来年のAdvent Calenderなどで発表して自慢しましょう。
明日はあかつきみさきさんで、スクリプトでなんかこうしてこうするの予定です。お楽しみに。