Bayes BPM Counter (ベイズBPM計測器) を公開しました
曲に合わせてスペースキーを押すか画面をタップするとBPMを推定します。下の画像クリックでジャンプします。
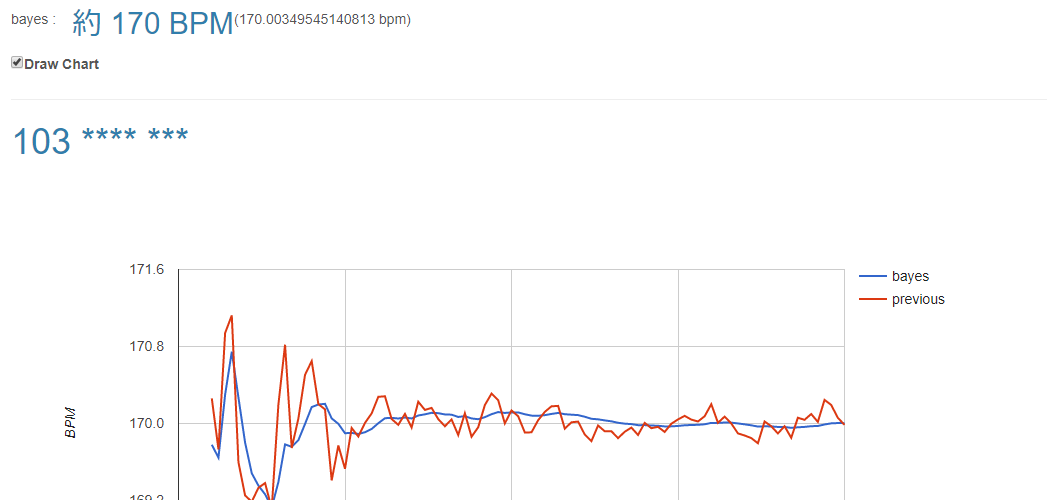
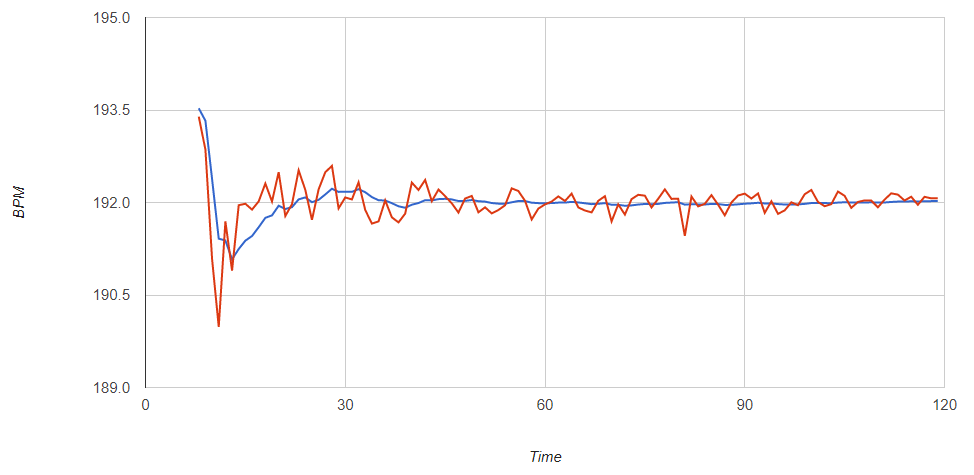
従来手法との比較
実際にやってみた結果です。横軸がキー入力回数で、縦軸が推定されたBPMになります。赤色が従来手法で、青色が今回のアルゴリズムです。従来手法と比較すると、収束が速いことがわかります。
理論的な話
1拍の長さと1拍目の時刻の事前分布を一様分布とし、キー入力の分布を正規分布として計算しました。詳しくは次回以降の記事でお話しようと思います(多分)。ベイズの定理に従って真の1拍の長さと真のBPMの期待値を計算をすると、キーが入力された時刻を
\[ T_n \quad (0 \leq n \leq N) \]
(ミリ秒)として、次のようになります。
\[ E = \frac{6}{N(N+1)(N+2)} \times \sum_{i=0}^{N} (2i-N)T_i \]
\[ \mathrm{BPM} = \frac{60000}{E} \]
ここで、キー入力の間隔を
\[ a_n = T_{n+1} – T_n \quad (0 \leq n \leq N – 1)\]
と置くと、上の $ E $ は次のように書き換えられます。
\[ E = \frac{6}{N(N+1)(N+2)} \times \sum_{i=0}^{N-1} (N-i)(i+1)a_i \]
$ a_i $ の係数の具体的な値は次のようになります。
| i=0 | i=1 | i=2 | i=3 | i=4 | i=5 | |
|---|---|---|---|---|---|---|
| N=1 | 1 | |||||
| N=2 | 2 | 2 | ||||
| N=3 | 3 | 4 | 3 | |||
| N=4 | 4 | 6 | 6 | 4 | ||
| N=5 | 5 | 8 | 9 | 8 | 5 | |
| N=6 | 6 | 10 | 12 | 12 | 10 | 6 |
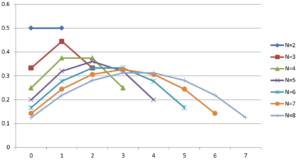
係数の和が1になるように正規化してプロットすると次のようになります。
従来手法との比較
従来の手法では、この式の代わりに次のような式を使用していました。
\[ E = \frac{1}{N} \times \sum_{i=0}^{N-1} a_i \]
これはキー押下間隔の相加平均で、$ a_n = T_{n+1} – T_n $ を代入すると次のようになります。
\[ E = \frac{1}{N} \times ( T_N – T_0 ) \]
この式は、最初のキー入力と最後のキー入力以外の時刻が計算結果に影響していないことを示します。これは得られた情報を最大限に利用してBPM推定するアルゴリズムとは考えづらいと言えます。
作った理由
「なんか最初と最後に押した時間しか反映されないのって変じゃないですか!?」

![[確率・統計] 中心極限定理:6面サイコロをn回振ったときの、出た目の和の確率分布](https://yuinore.net/wp-content/themes/customizr/assets/front/img/thumb-standard-empty.png)