惑星の間の平均距離
円軌道を描く2つの惑星の間の距離の時間平均を求める
惑星は公転をしているため、惑星間の距離は必ずしも一定ではない。惑星間の平均距離がどのような値になるのかを、単純な計算で調べてみる。
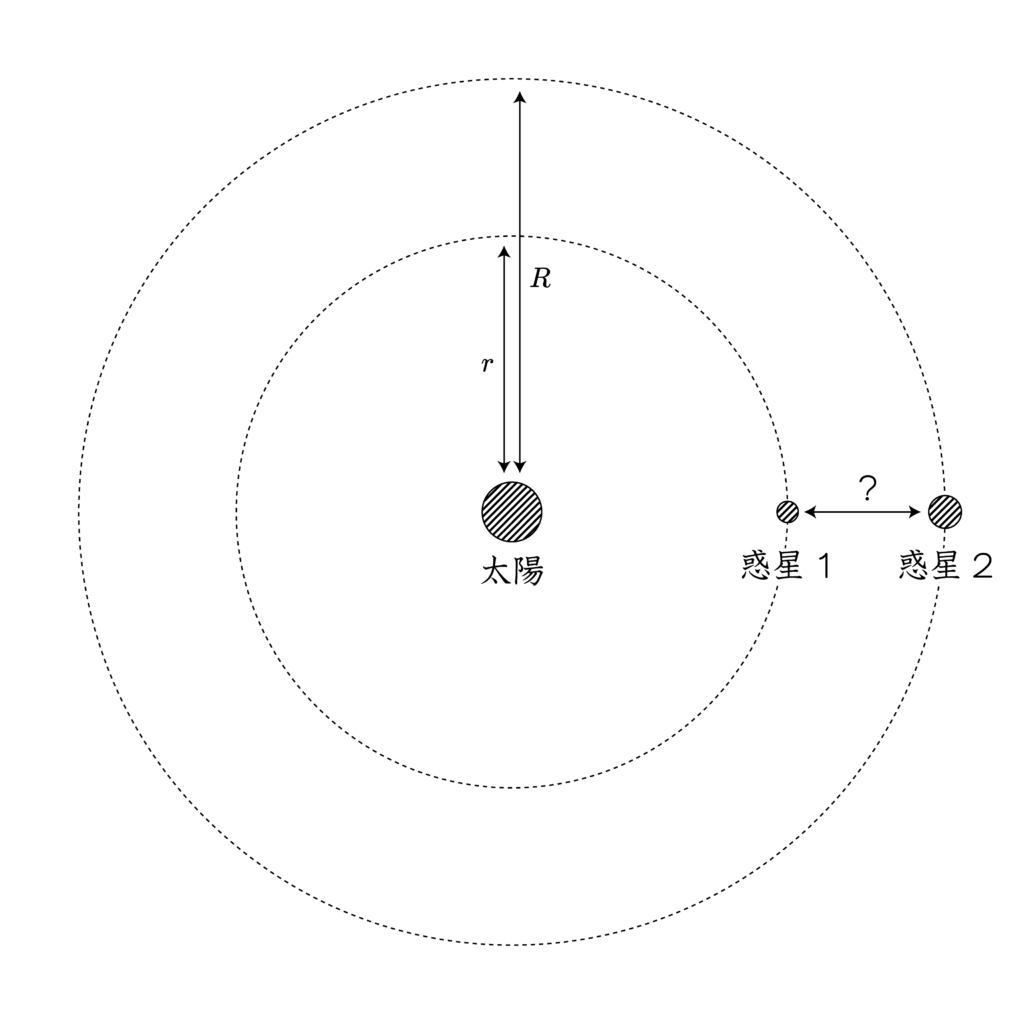
簡単のため、太陽の質量は十分大きく、かつ、惑星は完全な円軌道を描くものとする。また、惑星は同一平面上を周回しているものとする。
加えて、2つの惑星の軌道半径を $r, R$ とするとき、
$$0 < r \le R$$
を満たすものとする。
(i) 惑星1と惑星2の公転周期が等しい場合
この場合、天体間の相対位置は変化しない。以下のように $\theta$ を設定する。
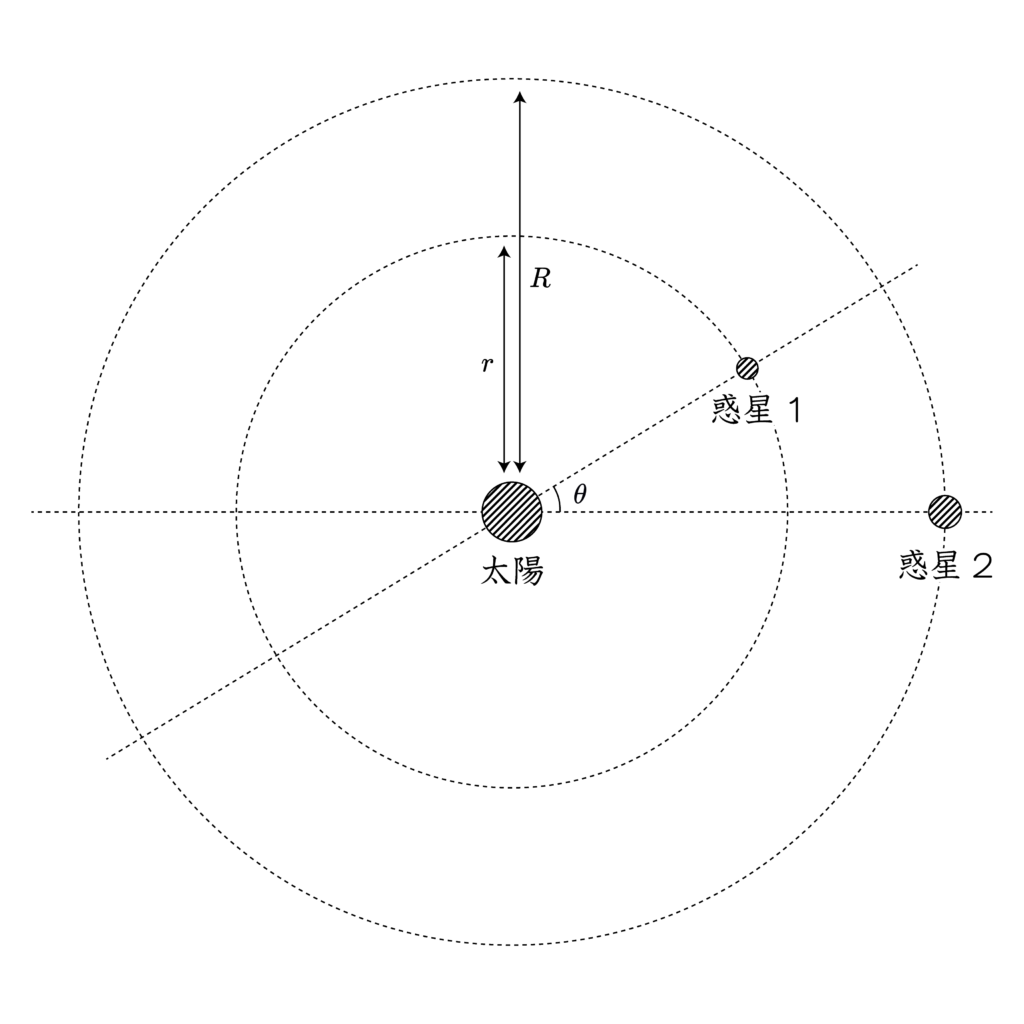
このとき、惑星間の距離は、
\begin{equation}
\begin{split}
d &= \sqrt{(R-r\cos\theta)^2+(r\sin\theta)^2} \\
&=\sqrt{R^2+r^2-2Rr\cos\theta} \\
\end{split}
\end{equation}
となる。
なお、現実ではケプラーの第三法則より $R=r$ の場合に限られる。
(ii) 惑星1と惑星2の公転周期が異なる場合
この場合、必ず一定時間ごとに天体間の相対位置が初期状態に戻る。相対位置のみに着目し、太陽と惑星2を固定して、惑星1が初期位置に戻るまでの距離の平均を考えることにする。
また、惑星が円軌道を描くとき、惑星の速度は一定なので、時間平均の代わりに $\theta$ を 0 から 2π まで積分して求めることにする。
このときの惑星間の平均距離は、
$$
\begin{equation}
\begin{split}
\bar{d} &= \frac{1}{2\pi}\int_0^{2\pi} \sqrt{(R-r\cos\theta)^2+(r\sin\theta)^2} \:\mathrm{d}\theta \\
&= \frac{1}{2\pi}\int_0^{2\pi} \sqrt{R^2+r^2-2Rr\cos\theta} \:\mathrm{d}\theta \\
&= \frac{1}{2\pi}\int_0^{2\pi} \sqrt{R^2+r^2+2Rr-4Rr\cos^2\frac{\theta}{2}} \:\mathrm{d}\theta \\
&= \frac{R+r}{2\pi}\int_0^{2\pi} \sqrt{1-\frac{4Rr}{(R+r)^2}\cos^2\frac{\theta}{2}} \:\mathrm{d}\theta \\
&= \frac{R+r}{\pi}\int_0^{\pi} \sqrt{1-\frac{4Rr}{(R+r)^2}\cos^2\phi} \:\mathrm{d}\phi \\
&= \frac{2(R+r)}{\pi}\int_0^{\pi/2} \sqrt{1-\frac{4Rr}{(R+r)^2}\sin^2\phi} \:\mathrm{d}\phi \\
\end{split}
\end{equation}
$$
となり、楕円積分に帰着することがわかる。
幾何的な考察
しかし、それだけでは面白味がないので、楕円の周と比較することで幾何的な考察をしてみたいと思う。
長半径 $a$、短半径 $b \:\: (\le a)$ の楕円の全周 $4L$ を第二種完全楕円積分を用いて表すと、
$$
4L = 4a\int_0^{\pi/2} \sqrt{1-k^2\sin^2\phi} \:\mathrm{d}\phi
$$
となる。ただし、k は離心率であり、
$$
k=\sqrt{\frac{a^2-b^2}{a^2}}
$$
である。この楕円の全周と惑星間の平均距離が等しいとするとき、つまり、
$$
\bar{d} = 4L
$$
とするとき、係数を比較すると、
$$
a=\frac{R+r}{2\pi}
$$
$$
b=\frac{R-r}{2\pi}
$$
という、解のうちのひとつが得られる。つまり、惑星間の平均距離 $\bar{d}$ は、長半径 $(R+r)/2\pi$、短半径 $(R-r)/2\pi$ の楕円の全周に等しいということである。(ただし、 b=0 の場合でも第二種完全楕円積分は成立し、等式が成り立つ。幾何的には長さ 2a の線分 2個であるとみなすことにする。)
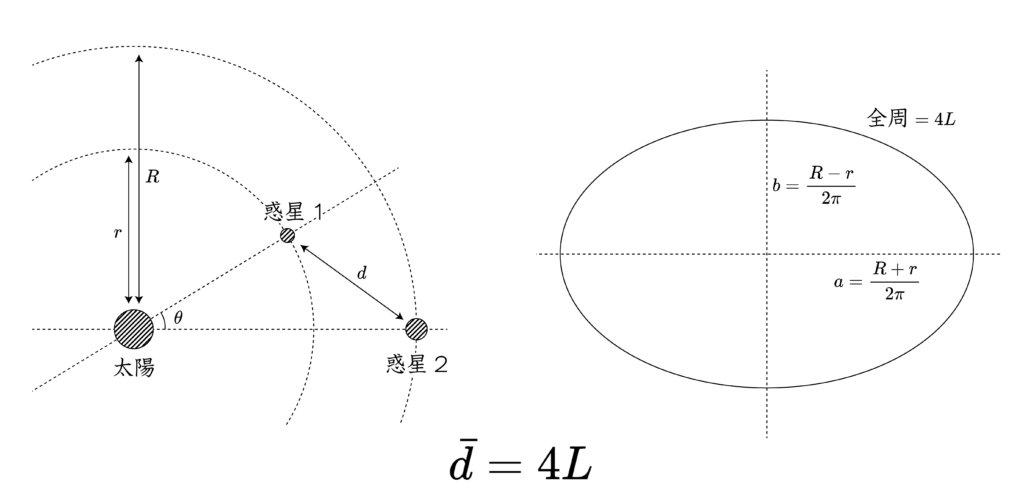
もし $r \ll R$ の場合、惑星間の平均距離は
$$
\bar{d} = R
$$
となる。また、$r=R$ の場合、惑星間の平均距離は
$$
\begin{equation}
\begin{split}
\bar{d} &= \frac{2(R+r)}{\pi}\int_0^{\pi/2} \sqrt{1-\frac{4Rr}{(R+r)^2}\sin^2\phi} \:\mathrm{d}\phi \\
&= \frac{4R}{\pi}\int_0^{\pi/2}\sqrt{1-\sin^2\phi} \:\mathrm{d}\phi\\
&= \frac{4}{\pi}R\\
\end{split}
\end{equation}
$$
となる。
(参考1) 下限と上限の見積もり
惑星間の平均距離の幾何的な表現は分かったが、もう少し、この結果について考察したいと思う。
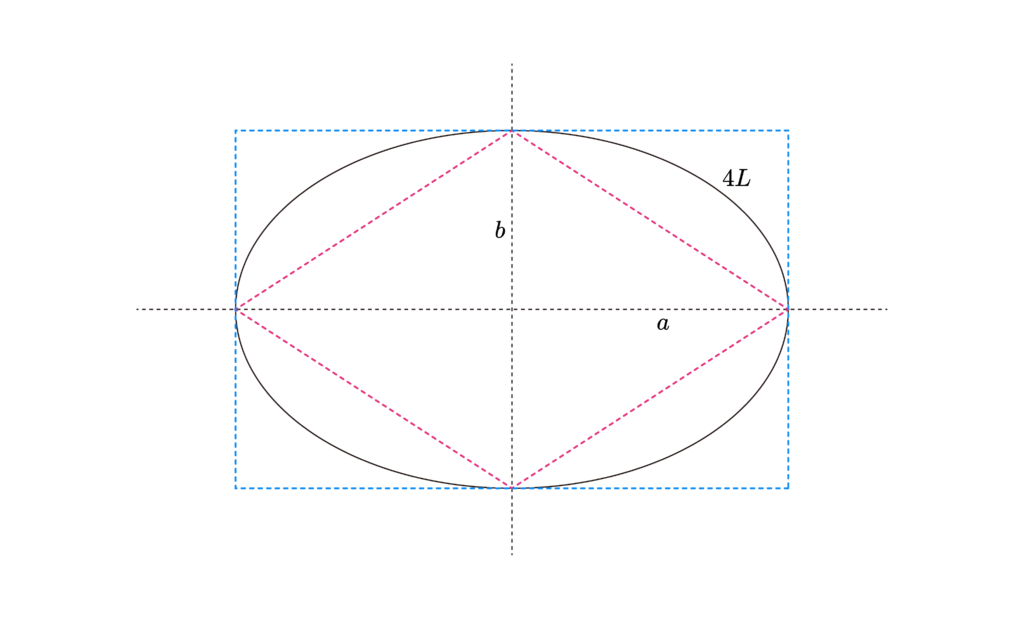
楕円の全周は楕円に内接するひし形の周よりも長いはずなので、
$$
\begin{equation}
\begin{split}
4L &> 4\sqrt{a^2+b^2}\\
&= \frac{2}{\pi}\sqrt{(R+r)^2+(R-r)^2}\\
&= \frac{4}{\pi}\sqrt{\frac{R^2+r^2}{2}}\\
\end{split}
\end{equation}
$$
また、外接する長方形の周よりも短いはずなので、
$$
\begin{equation}
\begin{split}
4L &< 4(a+b)\\
&= \frac{4}{\pi}R\\
\end{split}
\end{equation}
$$
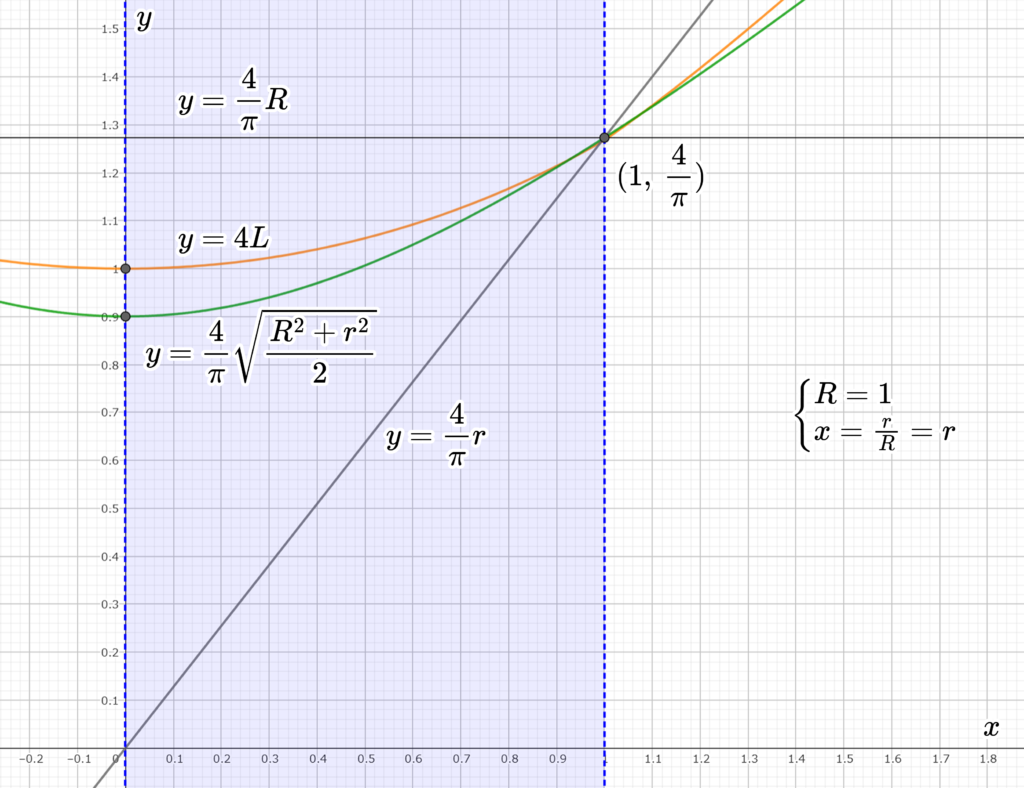
となる。まとめると、$R \ne r$ のとき、
$$
r
< \frac{4}{\pi}r
< \frac{4}{\pi}\sqrt{\frac{R^2+r^2}{2}}
< \bar{d} = 4L
< \frac{4}{\pi}R
$$
となる。($r=R$ の場合は楕円にならないため不等式が成立しないが、式に等号を含めると成立する。)
$R=1$ を固定して、x軸方向に $r$ を取ってグラフにすると以下のようになる。ただし、 $0 < x < 1$ である。
(参考2) 惑星間の距離の2乗平均平方根
ちなみに、惑星間の距離の2乗平均平方根はより簡単に計算できて、
$$
\begin{equation}
\begin{split}
\sqrt{\overline{d^2}} &= \sqrt{\frac{1}{2\pi}\int_0^{2\pi} \left\{(R-r\cos\theta)^2+(r\sin\theta)^2\right\} \:\mathrm{d}\theta} \\
&= \sqrt{\frac{1}{2\pi}\int_0^{2\pi} (R^2+r^2-2Rr\cos\theta) \:\mathrm{d}\theta} \\
&= \sqrt{\frac{1}{2\pi}\int_0^{2\pi} (R^2+r^2) \:\mathrm{d}\theta} \\
&= \sqrt{R^2+r^2} \\
\end{split}
\end{equation}
$$
となる。
感想
後になって調べてみたところ、太陽系惑星、特に水星の離心率や軌道傾斜角は意外と小さくないということが分かって驚いた。機会があったらより正確な平均距離も数値計算してみたいと思う。
参考資料
楕円積分 – Wikipedia
https://ja.wikipedia.org/wiki/楕円積分
太陽諸定数表/惑星諸定数表
https://japanknowledge.com/contents/common/solarplanet.html
軌道傾斜角 – Wikipedia
https://ja.wikipedia.org/wiki/軌道傾斜角
軌道離心率 – Wikipedia
https://ja.wikipedia.org/wiki/軌道離心率
3D Solar System Viewer | TheSkyLive.com
https://theskylive.com/3dsolarsystem
(参考3) 2025/1/28追記
後になって同様の内容の記事をいくつか見つけたので追記しておく。上の GIGAZINE の記事では、惑星間の平均距離が軌道半径の差 $R-r$ ではないということが日本語で分かりやすく説明されている。記事の最後には、太陽系の惑星間の平均距離の一覧表も添付されている。修正された計算手法は「ポイントサークル法」と呼ばれているとのこと。また、下の動画では数値計算によるシミュレーションを行い、惑星間の実際の距離と時間平均がアニメーションによって分かりやすく示されている。
「金星は地球に最も近い惑星ではない」という主張、ではどの惑星が地球に最も近いのか? – GIGAZINE
https://gigazine.net/news/20190313-earths-neighbor-is-not-venus/
Mercury is the closest planet to all seven other planets
惑星の間の平均距離
円軌道を描く2つの惑星の間の距離の時間平均を求める
惑星は公転をしているため、惑星間の距離は必ずしも一定ではない。惑星間の平均距離がどのような値になるのかを、単純な計算で調べてみる。
簡単のため、太陽の質量は十分大きく、かつ、惑星は完全な円軌道を描くものとする。また、惑星は同一平面上を周回しているものとする。
加えて、2つの惑星の軌道半径を $r, R$ とするとき、
$$0 < r \le R$$ を満たすものとする。
(i) 惑星1と惑星2の公転周期が等しい場合
この場合、天体間の相対位置は変化しない。以下のように $\theta$ を設定する。
このとき、惑星間の距離は、
\begin{equation}
\begin{split}
d &= \sqrt{(R-r\cos\theta)^2+(r\sin\theta)^2} \\
&=\sqrt{R^2+r^2-2Rr\cos\theta} \\
\end{split}
\end{equation}
となる。
なお、現実ではケプラーの第三法則より $R=r$ の場合に限られる。
(ii) 惑星1と惑星2の公転周期が異なる場合
この場合、必ず一定時間ごとに天体間の相対位置が初期状態に戻る。相対位置のみに着目し、太陽と惑星2を固定して、惑星1が初期位置に戻るまでの距離の平均を考えることにする。
また、惑星が円軌道を描くとき、惑星の速度は一定なので、時間平均の代わりに $\theta$ を 0 から 2π まで積分して求めることにする。
このときの惑星間の平均距離は、
$$
\begin{equation}
\begin{split}
\bar{d} &= \frac{1}{2\pi}\int_0^{2\pi} \sqrt{(R-r\cos\theta)^2+(r\sin\theta)^2} \:\mathrm{d}\theta \\
&= \frac{1}{2\pi}\int_0^{2\pi} \sqrt{R^2+r^2-2Rr\cos\theta} \:\mathrm{d}\theta \\
&= \frac{1}{2\pi}\int_0^{2\pi} \sqrt{R^2+r^2+2Rr-4Rr\cos^2\frac{\theta}{2}} \:\mathrm{d}\theta \\
&= \frac{R+r}{2\pi}\int_0^{2\pi} \sqrt{1-\frac{4Rr}{(R+r)^2}\cos^2\frac{\theta}{2}} \:\mathrm{d}\theta \\
&= \frac{R+r}{\pi}\int_0^{\pi} \sqrt{1-\frac{4Rr}{(R+r)^2}\cos^2\phi} \:\mathrm{d}\phi \\
&= \frac{2(R+r)}{\pi}\int_0^{\pi/2} \sqrt{1-\frac{4Rr}{(R+r)^2}\sin^2\phi} \:\mathrm{d}\phi \\
\end{split}
\end{equation}
$$
となり、楕円積分に帰着することがわかる。
幾何的な考察
しかし、それだけでは面白味がないので、楕円の周と比較することで幾何的な考察をしてみたいと思う。
長半径 $a$、短半径 $b \:\: (\le a)$ の楕円の全周 $4L$ を第二種完全楕円積分を用いて表すと、
$$
4L = 4a\int_0^{\pi/2} \sqrt{1-k^2\sin^2\phi} \:\mathrm{d}\phi
$$
となる。ただし、k は離心率であり、
$$
k=\sqrt{\frac{a^2-b^2}{a^2}}
$$
である。この楕円の全周と惑星間の平均距離が等しいとするとき、つまり、
$$
\bar{d} = 4L
$$
とするとき、係数を比較すると、
$$
a=\frac{R+r}{2\pi}
$$
$$
b=\frac{R-r}{2\pi}
$$
という、解のうちのひとつが得られる。つまり、惑星間の平均距離 $\bar{d}$ は、長半径 $(R+r)/2\pi$、短半径 $(R-r)/2\pi$ の楕円の全周に等しいということである。(ただし、 b=0 の場合でも第二種完全楕円積分は成立し、等式が成り立つ。幾何的には長さ 2a の線分 2個であるとみなすことにする。)
もし $r \ll R$ の場合、惑星間の平均距離は
$$
\bar{d} = R
$$
となる。また、$r=R$ の場合、惑星間の平均距離は
$$
\begin{equation}
\begin{split}
\bar{d} &= \frac{2(R+r)}{\pi}\int_0^{\pi/2} \sqrt{1-\frac{4Rr}{(R+r)^2}\sin^2\phi} \:\mathrm{d}\phi \\
&= \frac{4R}{\pi}\int_0^{\pi/2}\sqrt{1-\sin^2\phi} \:\mathrm{d}\phi\\
&= \frac{4}{\pi}R\\
\end{split}
\end{equation}
$$
となる。
(参考1) 下限と上限の見積もり
惑星間の平均距離の幾何的な表現は分かったが、もう少し、この結果について考察したいと思う。
楕円の全周は楕円に内接するひし形の周よりも長いはずなので、
$$
\begin{equation}
\begin{split}
4L &> 4\sqrt{a^2+b^2}\\
&= \frac{2}{\pi}\sqrt{(R+r)^2+(R-r)^2}\\
&= \frac{4}{\pi}\sqrt{\frac{R^2+r^2}{2}}\\
\end{split}
\end{equation}
$$
また、外接する長方形の周よりも短いはずなので、
$$
\begin{equation}
\begin{split}
4L &< 4(a+b)\\ &= \frac{4}{\pi}R\\ \end{split} \end{equation} $$ となる。まとめると、$R \ne r$ のとき、 $$ r < \frac{4}{\pi}r < \frac{4}{\pi}\sqrt{\frac{R^2+r^2}{2}} < \bar{d} = 4L < \frac{4}{\pi}R $$ となる。($r=R$ の場合は楕円にならないため不等式が成立しないが、式に等号を含めると成立する。)
$R=1$ を固定して、x軸方向に $r$ を取ってグラフにすると以下のようになる。ただし、 $0 < x < 1$ である。
(参考2) 惑星間の距離の2乗平均平方根
ちなみに、惑星間の距離の2乗平均平方根はより簡単に計算できて、
$$
\begin{equation}
\begin{split}
\sqrt{\overline{d^2}} &= \sqrt{\frac{1}{2\pi}\int_0^{2\pi} \left\{(R-r\cos\theta)^2+(r\sin\theta)^2\right\} \:\mathrm{d}\theta} \\
&= \sqrt{\frac{1}{2\pi}\int_0^{2\pi} (R^2+r^2-2Rr\cos\theta) \:\mathrm{d}\theta} \\
&= \sqrt{\frac{1}{2\pi}\int_0^{2\pi} (R^2+r^2) \:\mathrm{d}\theta} \\
&= \sqrt{R^2+r^2} \\
\end{split}
\end{equation}
$$
となる。
感想
後になって調べてみたところ、太陽系惑星、特に水星の離心率や軌道傾斜角は意外と小さくないということが分かって驚いた。機会があったらより正確な平均距離も数値計算してみたいと思う。
参考資料
(参考3) 2025/1/28追記
後になって同様の内容の記事をいくつか見つけたので追記しておく。上の GIGAZINE の記事では、惑星間の平均距離が軌道半径の差 $R-r$ ではないということが日本語で分かりやすく説明されている。記事の最後には、太陽系の惑星間の平均距離の一覧表も添付されている。修正された計算手法は「ポイントサークル法」と呼ばれているとのこと。また、下の動画では数値計算によるシミュレーションを行い、惑星間の実際の距離と時間平均がアニメーションによって分かりやすく示されている。