x^2 + y^2 を上から抑えるのは x, y をそれぞれ抑えるよりも強い

2乗和 x^2 + y^2 を上から抑えるのは、それぞれの成分を上から抑えるよりも強い

この記事では以下を示す。ただし x, y, k は実数とする。

$$
x^2+y^2 \ll k^2 \:\: \Rightarrow \:\: x^2 \ll k^2
$$

$$
x^2+y^2 \ll k^2 \:\: \Rightarrow \:\: y^2 \ll k^2
$$

$$
x^2+y^2 \ll k^2 \:\: \Rightarrow \:\: |xy| \ll k^2
$$

証明

$$
x^2 \le x^2+y^2 \ll k^2
$$

$$
y^2 \le x^2+y^2 \ll k^2
$$

また、 $|x| \le |y|$ のとき

$$
|xy| = |x||y| \le y^2 \le x^2+y^2 \ll k^2
$$

であり、 $|y| \le |x|$ のとき

$$
|xy| = |x||y| \le x^2 \le x^2+y^2 \ll k^2
$$

証明終了。

図示

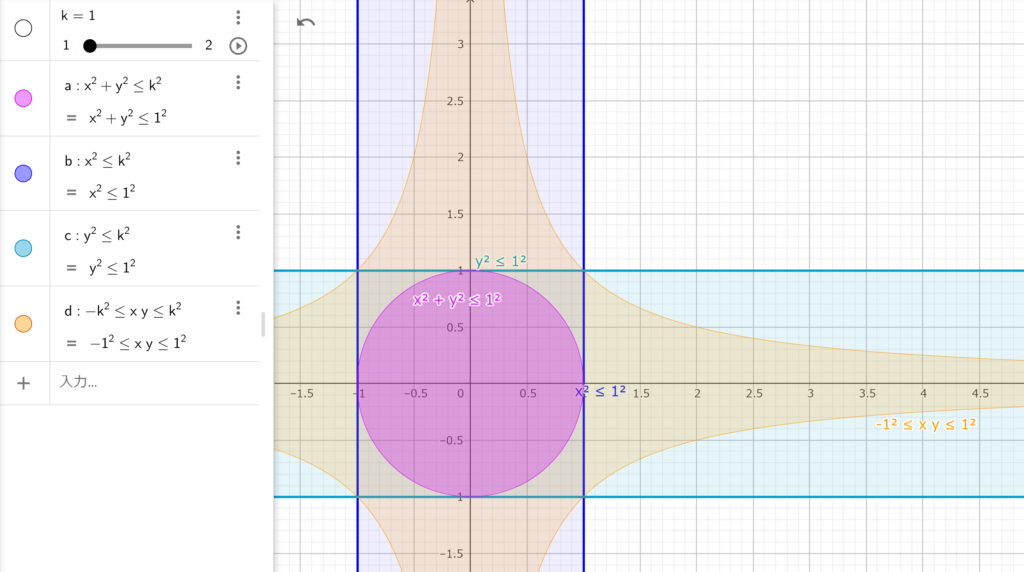
以下に、k = 1 の場合の 4 つの領域

$$ a : x^2 + y^2 \le k^2 $$

$$ b : x^2 \le k^2 $$

$$ c : y^2 \le k^2 $$

$$ d : |xy| \le k^2 $$

および境界線を図示する。領域の包含関係を確認することにより、左辺の大小関係を調べることができる。

グラフを作ってて気付いたおまけとアニメーション

なお、さらに強い

$$
2|xy| \le x^2+y^2
$$

が成立する。これは、 $xy \ge 0$ のとき、

$$
x^2+y^2-2|xy| = x^2+y^2-2xy =(x-y)^2 \ge 0
$$

$xy \le 0$ のとき、

$$
x^2+y^2-2|xy| = x^2+y^2+2xy =(x+y)^2 \ge 0
$$

となり、簡単に示せる。

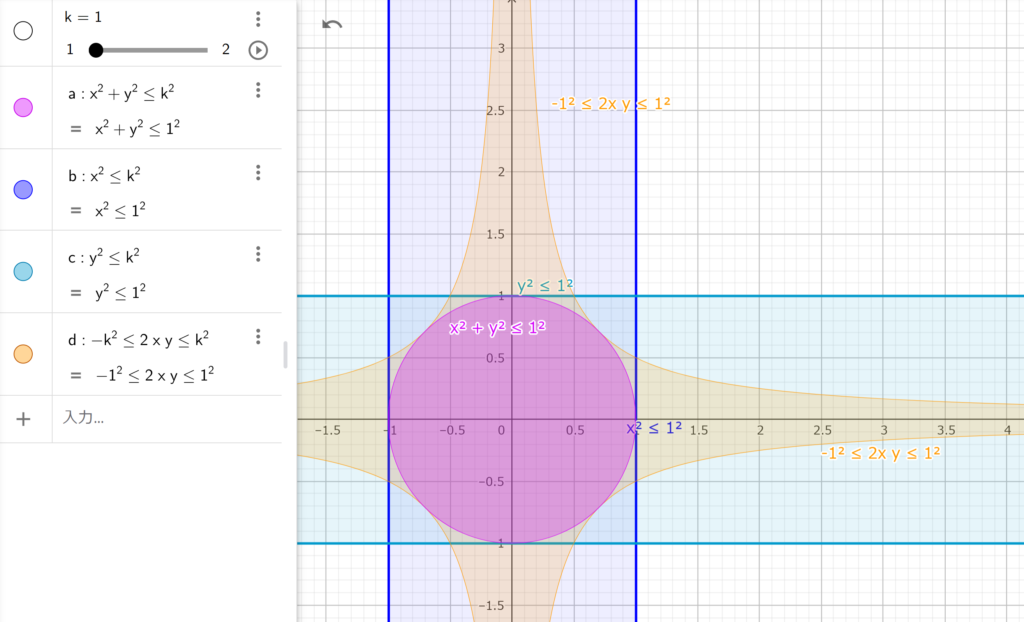
k を 1 から 2 まで変化させた場合のアニメーション。すべての項が2次なので、ただスケーリングしてるだけですね。

3D に図示するとこんな感じ。赤い面は円錐状になっていて、他のどの面よりも上にあることがわかる。

相乗平均、相加平均、2乗平均の大小関係

ちなみに、一般に (相乗平均) ≦ (相加平均) ≦ (2乗平均) が成り立つそうです。

(2乗平均)≧(相加平均)≧(相乗平均)≧(調和平均)の証明
https://examist.jp/mathematics/expression-proof/soukasoujyou-syoumei/

最初からこの記事を見れば良かったですね、皆さんはこっちを読んでください。