【小ネタ】斜投影図法を使用した3次元から2次元の投影変換

投影変換について調べていたところ、興味深い図法についての記載があったため、こちらについても考えてみたい。

斜投影図法
平行光線を利用して、投影面に平行に置いた物体の形を1つの投影面に斜めに表す図法です。
http://i-zukan.net/ic/pe_projection.htm

この図法にそんな名前が付いていたなんて知らなかった……。

さて、斜投影図法や、その一種であるキャビネット図は、平行投影（直投影）がそうであるように、カメラを通して実際に再現することが難しい図法である。この図法では投影線が互いに平行で、透視投影のように1点で交わらない。平行投影が望遠カメラの画角を小さくした際の極限として導くことができるのと同じように、斜投影図法もある種の極限として実現することができる。

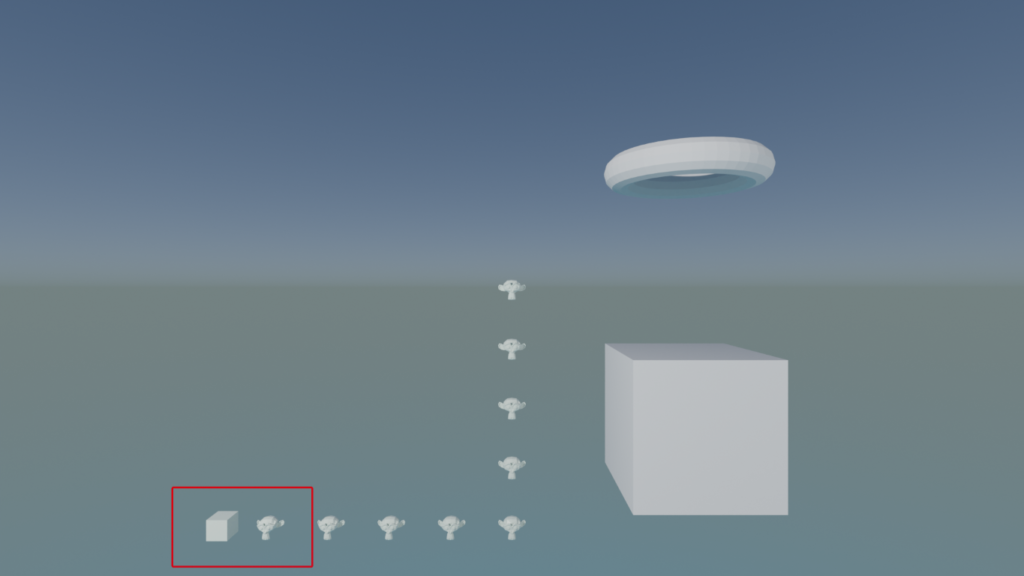
上の図の赤い枠で囲まれた部分を拡大した図：

変換の手順

1. 頂点の回転と平行移動

レンダリングしたい点のワールド座標を p とする。

$$\vec{p}=(p_x,p_y,p_z)$$

カメラの視点が原点、カメラの注視点が z 軸の正の方向、カメラの上方向が y 軸の正の方向になるように頂点を回転・平行移動する。ただし、カメラが既にこの条件を満たしている場合はこの変換を行う必要はない。

$$\vec{q}=R_{\mathrm{camera}}^{-1}\cdot(\vec{p}-\vec{p}_{\mathrm{camera}})$$

2. スクリーン座標への投影変換

キャビネット図では幅：高さ：奥行きの（スクリーン座標系におおける長さの）比率が $1:1:1/2$ となる。奥行き方向の傾斜を45度とする。z 軸に平行な直線について考えたとき、z 成分が 1 増えると、スクリーン座標の x, y 成分はそれぞれ $1/(2\sqrt{2})$ ずつ増えることになる。

$$\varDelta q_z : \varDelta s_x = 1:\frac{1}{2\sqrt{2}}$$

$$\varDelta q_z : \varDelta s_y = 1:\frac{1}{2\sqrt{2}}$$

従って、スクリーン座標は $z_0$ を定数として、

$$\vec{s} = (q_x + \frac{q_z-z_0}{2\sqrt{2}}, \: q_y + \frac{q_z-z_0}{2\sqrt{2}})$$

となる。$z_0$ の値は平行移動の差でしかないので、これを無視すれば、単に

$$\vec{s} = (q_x + \frac{q_z}{2\sqrt{2}}, \: q_y + \frac{q_z}{2\sqrt{2}})$$

となる。

これ記事にするほどの内容ではなかったかもしれない……。

投影 (図学) – Wikipedia
https://ja.wikipedia.org/wiki/投影_(図学)#投影線

余談

カメラを使用して正射投影（平行投影）で撮影するシステムは既にあるらしい。

正射投影撮像システム
最大器高100cmの遺物を1億2千万画素の高精細な正射投影で撮影しオルソ画像を生成いたします。
https://www.shin-eng.co.jp/cultural/sios/

テレセントリックレンズチュートリアル
https://www.thorlabs.co.jp/newgrouppage9.cfm?objectgroup_id=10762

テレセントリックレンズについて（2024年5回目）
http://www.ned-sensor.com/about_telecentric_20240501/