3次元から2次元への射影変換の考え方の入門部分
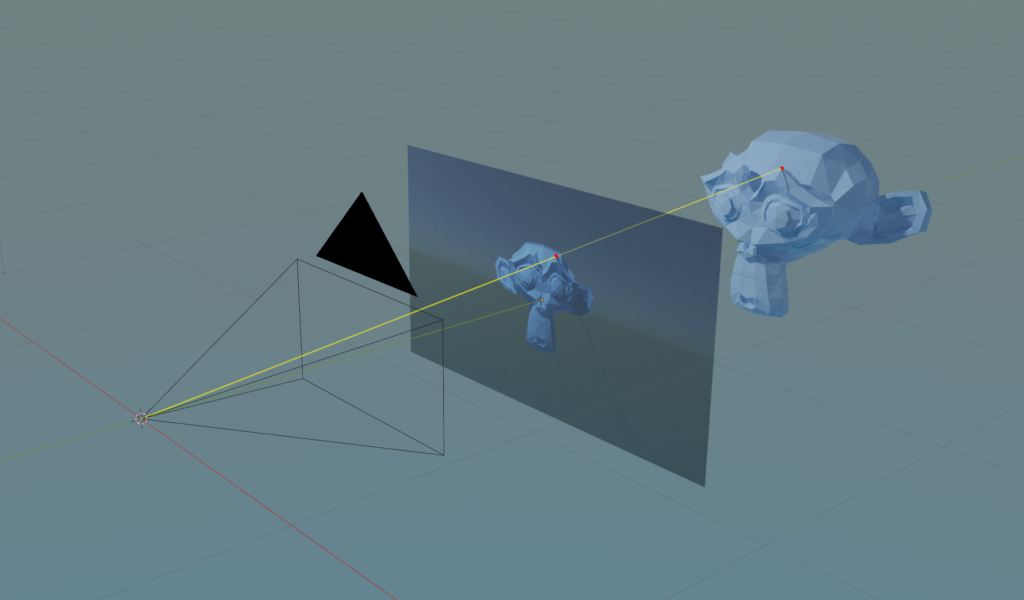
この記事では、3DCG のレンダリングで取り扱われているような平行投影・透視投影を行う場合にどのような計算を行えばよいのかについて説明する。空間上の点があるとき、それを出力画面における座標に変換する方法を説明する。コンピューターグラフィックスにおける実際の計算とは異なるが、考え方の基本部分は同じである。
簡単のため、この記事では、z 深度や深度によるクリッピングを無視する。
Perspective/Orthographic(透視投影/平行投影) — Blender Manual
https://docs.blender.org/manual/ja/3.1/editors/3dview/navigate/projections.html
平行投影の場合
1. 頂点の回転と平行移動(ワールド座標系からビュー座標系への変換)
レンダリングしたい点のワールド座標を p とする。
$$\vec{p}=(p_x,p_y,p_z)$$
カメラの視点が原点、カメラの注視点が z 軸の正の方向、カメラの上方向が y 軸の正の方向になるように頂点を回転・平行移動する。ただし、カメラが既にこの条件を満たしている場合はこの変換を行う必要はない。
$$\vec{q}=R_{\mathrm{camera}}^{-1}\cdot(\vec{p}-\vec{p}_{\mathrm{camera}})$$
2. スクリーンへの投影
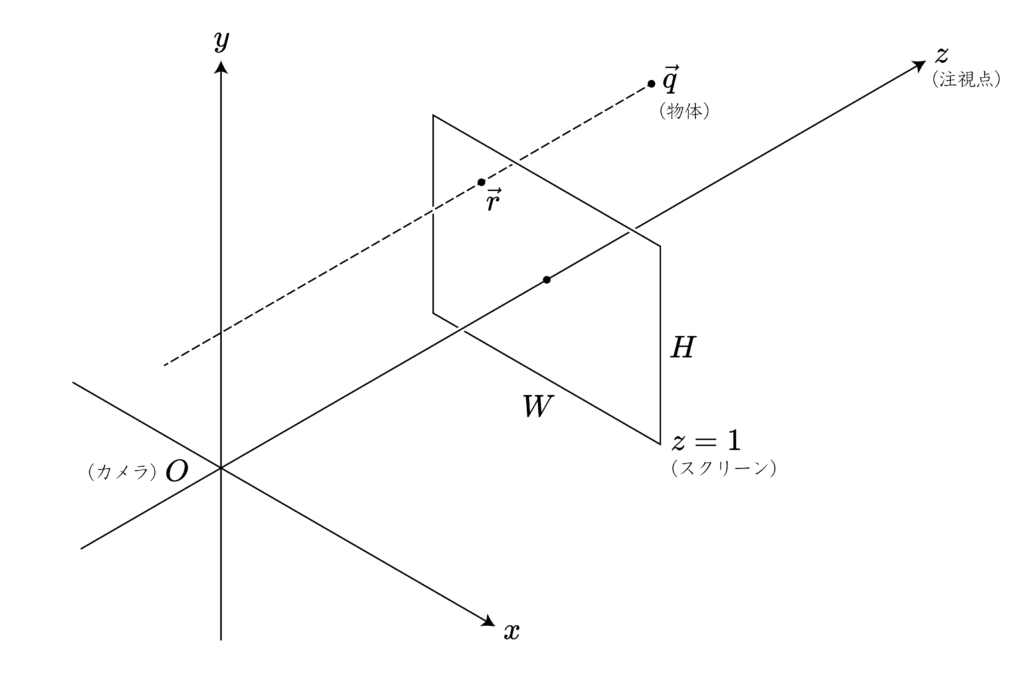
z 軸に平行な直線を引き、スクリーン (投影面) との交点を求める。
$$\vec{r} = (q_x,q_y,1)$$
3. x, y 成分の抽出
得られた頂点の x, y 成分を抽出する。(z 深度については今回は無視する。)
$$\vec{s} = (r_x,r_y)$$
4. 画角の変換
画面の幅、画面の高さに合わせてスケーリングすると、出力画面での相対位置が得られる。
$$\vec{t} = \left( \frac{s_x}{W}, \frac{s_y}{H} \right)$$
透視投影の場合
レンダリングしたい点のワールド座標を p とする。
$$\vec{p}=(p_x,p_y,p_z)$$
カメラの視点が原点、カメラの注視点が z 軸の正の方向、カメラの上方向が y 軸の正の方向になるように頂点を回転・平行移動する。ただし、カメラが既にこの条件を満たしている場合はこの変換を行う必要はない。
$$\vec{q}=R_{\mathrm{camera}}^{-1}\cdot(\vec{p}-\vec{p}_{\mathrm{camera}})$$
1. 頂点の回転と平行移動(ワールド座標系からビュー座標系への変換)
2. スクリーンへの投影
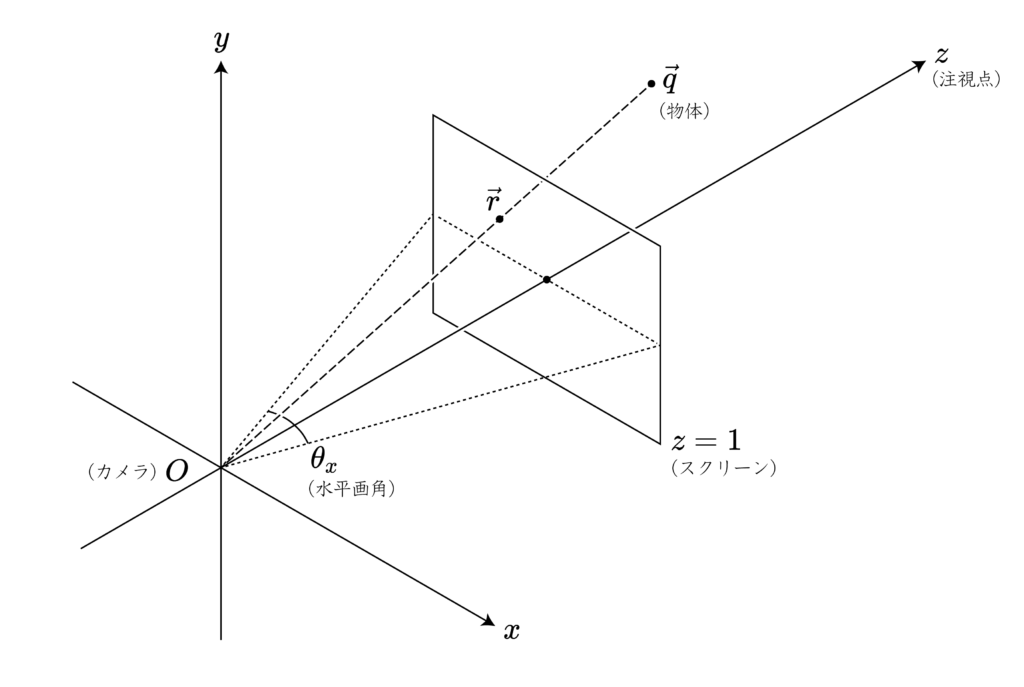
簡単のため、 $q_z>0$ を満たすものとする。
平面 $z=1$ をスクリーン (投影面) とし、レンダリングしたい物体がスクリーンにどのように投影されるかを考える。このためには、レンダリングしたい物体からカメラの視点に引いた直線 (投影線) が、スクリーンとどこで交わるかを考えればよい。
$$
\begin{cases}
\vec{r} = u\vec{q} + (1-u)\vec{O}\\
r_z=1\\
\end{cases}
$$
これを解くと、
$$\vec{r} = \left( \frac{q_x}{q_z}, \frac{q_y}{q_z}, 1 \right)$$
となる。
3. x, y 成分の抽出
得られた頂点の x, y 成分を抽出する。(z 深度については今回は無視する。)
$$\vec{s} = (r_x,r_y)$$
4. 画角の変換
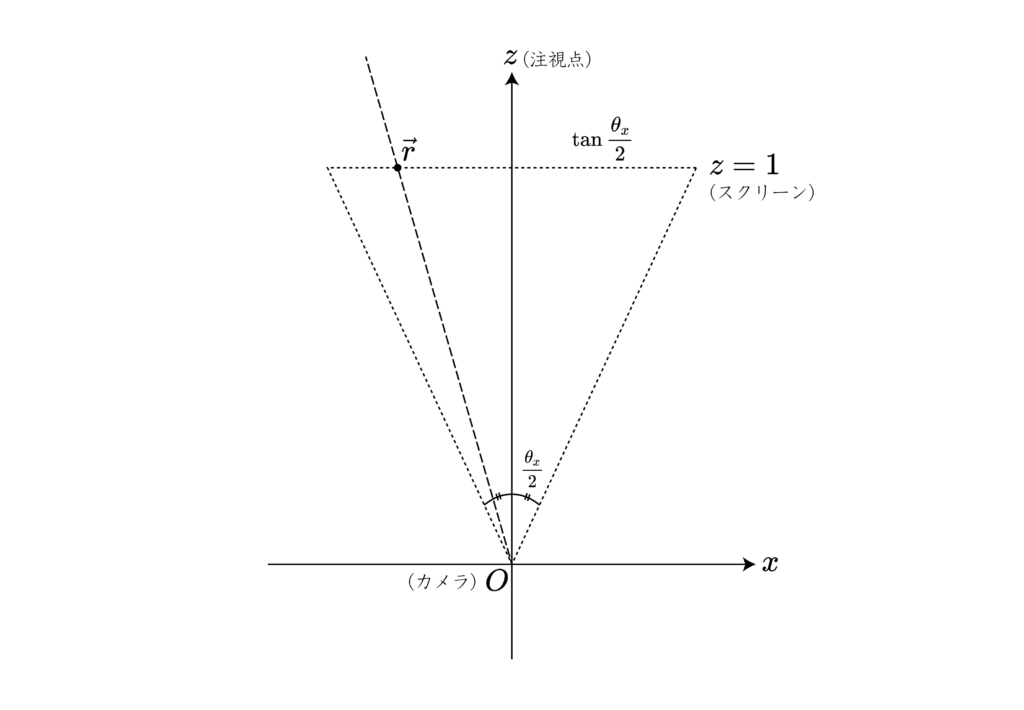
水平画角、垂直画角に合わせてスケーリングすると、出力画面での相対位置が得られる。いま、水平画角を $\theta_x$ 、垂直画角を $\theta_y$ とすると、
$$
\vec{t}=\left(
\frac{s_x}{2\tan(\theta_x/2)},
\frac{s_y}{2\tan(\theta_y/2)}
\right)
$$
ただし、通常はアスペクト比を保つようにスケーリングの比率を設定する。
$$W:H=\tan\frac{\theta_x}{2} : \tan\frac{\theta_y}{2}$$
補足
near 面と far 面(クリッピング範囲)をどのように設定するか、画角の設定方法、ビュー座標系のz軸の向きなどにより様々な形の式がある。加えて、通常は3DCGのレンダリングにおいては4次元のベクトルや行列(同次座標系)を使用してこの計算を行うため、実際に3DCGのレンダリングで上記の式がそのまま使用されるわけではない。
その70 完全ホワイトボックスなパースペクティブ射影変換行列
http://marupeke296.com/DXG_No70_perspective.html
透視投影変換行列の数学
https://qiita.com/ryutorion/items/0824a8d6f27564e850c9
3次元から2次元への射影変換の考え方の入門部分
この記事では、3DCG のレンダリングで取り扱われているような平行投影・透視投影を行う場合にどのような計算を行えばよいのかについて説明する。空間上の点があるとき、それを出力画面における座標に変換する方法を説明する。コンピューターグラフィックスにおける実際の計算とは異なるが、考え方の基本部分は同じである。
簡単のため、この記事では、z 深度や深度によるクリッピングを無視する。
平行投影の場合
1. 頂点の回転と平行移動(ワールド座標系からビュー座標系への変換)
レンダリングしたい点のワールド座標を p とする。
$$\vec{p}=(p_x,p_y,p_z)$$
カメラの視点が原点、カメラの注視点が z 軸の正の方向、カメラの上方向が y 軸の正の方向になるように頂点を回転・平行移動する。ただし、カメラが既にこの条件を満たしている場合はこの変換を行う必要はない。
$$\vec{q}=R_{\mathrm{camera}}^{-1}\cdot(\vec{p}-\vec{p}_{\mathrm{camera}})$$
2. スクリーンへの投影
z 軸に平行な直線を引き、スクリーン (投影面) との交点を求める。
$$\vec{r} = (q_x,q_y,1)$$
3. x, y 成分の抽出
得られた頂点の x, y 成分を抽出する。(z 深度については今回は無視する。)
$$\vec{s} = (r_x,r_y)$$
4. 画角の変換
画面の幅、画面の高さに合わせてスケーリングすると、出力画面での相対位置が得られる。
$$\vec{t} = \left( \frac{s_x}{W}, \frac{s_y}{H} \right)$$
透視投影の場合
レンダリングしたい点のワールド座標を p とする。
$$\vec{p}=(p_x,p_y,p_z)$$
カメラの視点が原点、カメラの注視点が z 軸の正の方向、カメラの上方向が y 軸の正の方向になるように頂点を回転・平行移動する。ただし、カメラが既にこの条件を満たしている場合はこの変換を行う必要はない。
$$\vec{q}=R_{\mathrm{camera}}^{-1}\cdot(\vec{p}-\vec{p}_{\mathrm{camera}})$$
1. 頂点の回転と平行移動(ワールド座標系からビュー座標系への変換)
2. スクリーンへの投影
簡単のため、 $q_z>0$ を満たすものとする。
平面 $z=1$ をスクリーン (投影面) とし、レンダリングしたい物体がスクリーンにどのように投影されるかを考える。このためには、レンダリングしたい物体からカメラの視点に引いた直線 (投影線) が、スクリーンとどこで交わるかを考えればよい。
$$
\begin{cases}
\vec{r} = u\vec{q} + (1-u)\vec{O}\\
r_z=1\\
\end{cases}
$$
これを解くと、
$$\vec{r} = \left( \frac{q_x}{q_z}, \frac{q_y}{q_z}, 1 \right)$$
となる。
3. x, y 成分の抽出
得られた頂点の x, y 成分を抽出する。(z 深度については今回は無視する。)
$$\vec{s} = (r_x,r_y)$$
4. 画角の変換
水平画角、垂直画角に合わせてスケーリングすると、出力画面での相対位置が得られる。いま、水平画角を $\theta_x$ 、垂直画角を $\theta_y$ とすると、
$$
\vec{t}=\left(
\frac{s_x}{2\tan(\theta_x/2)},
\frac{s_y}{2\tan(\theta_y/2)}
\right)
$$
ただし、通常はアスペクト比を保つようにスケーリングの比率を設定する。
$$W:H=\tan\frac{\theta_x}{2} : \tan\frac{\theta_y}{2}$$
補足
near 面と far 面(クリッピング範囲)をどのように設定するか、画角の設定方法、ビュー座標系のz軸の向きなどにより様々な形の式がある。加えて、通常は3DCGのレンダリングにおいては4次元のベクトルや行列(同次座標系)を使用してこの計算を行うため、実際に3DCGのレンダリングで上記の式がそのまま使用されるわけではない。