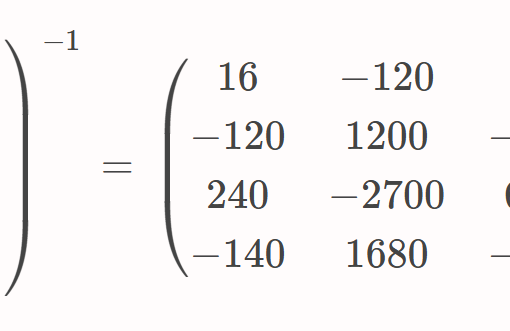関数 $f(x)$ が閉区間 $[0,1]$ で定義されているとき、この関数に対して二乗誤差が最小になる三次多項式を求める。
今回は簡単のため、 $f(x)$ は加算個の点を除いて連続で、かつ有界であるものとする。
三次多項式と二乗誤差
三次多項式を次の形で定義する。
$$
p(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3
$$
このとき、 $[0,1]$ 区間における二乗誤差は
$$
E(a_0,a_1,a_2,a_3) = \int_0^1 (f(x) \,-\, p(x))^2 \, \mathrm{d}x
$$
となる。これを最小化したい。
極値の計算
$E$ が最小値を取るためには、 $a_k$ による偏微分がすべて 0 になる必要がある。
$$
\frac{\partial E}{\partial a_k} = 0 \quad (k=0,1,2,3)
$$
この左辺は
$$
\frac{\partial E}{\partial a_k} = \frac{\partial}{\partial a_k} \int_0^1 (f(x) \,-\, p(x))^2 \, \mathrm{d}x
$$
となる。積分と偏微分を入れ替えて、
$$
\frac{\partial E}{\partial a_k} = \int_0^1 \frac{\partial}{\partial a_k} (f(x) \,-\, p(x))^2 \, \mathrm{d}x
$$
とし、また、二乗の中身の微分が
$$
\frac{\partial}{\partial a_k} (f(x) \,-\, p(x))
= 0 \,-\, \frac{\partial}{\partial a_k} p(x)
= – x^k
$$
であることを用いると、
$$
\frac{\partial E}{\partial a_k} = \int_0^1 2(f(x) \,-\, p(x))(-x^k) \, \mathrm{d}x = 0
$$
より、方程式
$$
\int_0^1 p(x) \, x^k \, \mathrm{d}x = \int_0^1 f(x) \, x^k \, \mathrm{d}x \quad (k=0,1,2,3)
$$
が得られる。
この方程式の解
左辺の積分を具体的に計算すると、以下のような連立一次方程式の形が得られる。
$$
\begin{pmatrix}
1 & \frac12 & \frac13 & \frac14 \\
\frac12 & \frac13 & \frac14 & \frac15 \\
\frac13 & \frac14 & \frac15 & \frac16 \\
\frac14 & \frac15 & \frac16 & \frac17
\end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \end{pmatrix} = \begin{pmatrix}
\int_0^1 f(x) \, \mathrm{d}x \\
\int_0^1 f(x)x \, \mathrm{d}x \\
\int_0^1 f(x)x^2 \, \mathrm{d}x \\
\int_0^1 f(x)x^3 \, \mathrm{d}x
\end{pmatrix}
$$
これを解けば、係数 $a_k$ を求めることができる。
ここで、左辺の行列の逆行列は存在して、
$$
\begin{pmatrix}
16 & -120 & 240 & -140 \\
-120 & 1200 & -2700 & 1680 \\
240 & -2700 & 6480 & -4200 \\
-140 & 1680 & -4200 & 2800
\end{pmatrix}
$$
となるため、これを用いる。
最小値になるか?
この計算から分かるように、極値がただひとつのみ存在しているため、この点で $E$ は最大値または最小値を取るが、直感的には最小値が存在することは明らかであり、最小値となる……と思う!!
でも $a_0 \to \infty$ で $E \to +\infty$ になることを示せば十分な気がする。
12/4 訂正 : 一変数関数の場合はそうだが、多変数の場合は鞍点となる場合があるため、最大値または最小値を取るとは限らない。
学部一年の内容だぞしっかりしてくれ
三次多項式以外の例
三次多項式以外でも、同様の計算方法で近似多項式を求めることができる。
計算例
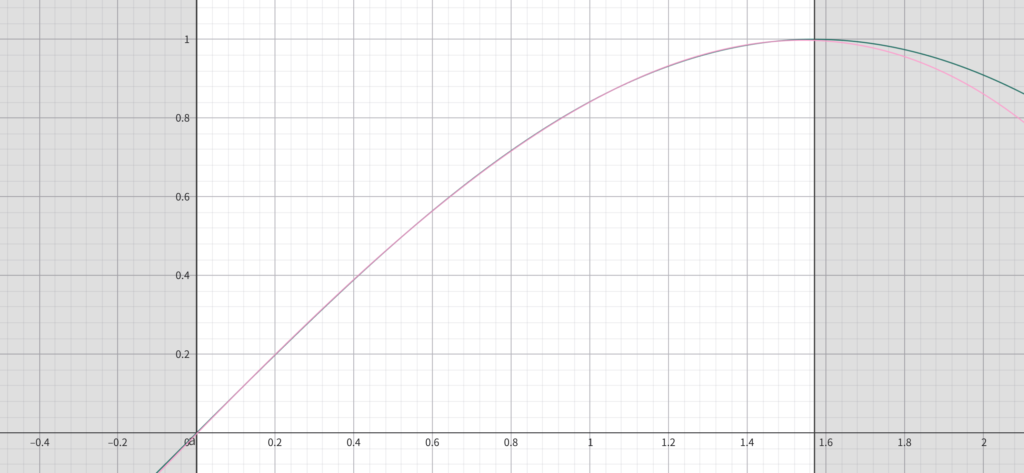
$$
f(x)=\sin \frac{\pi}{2} x
$$
のとき
$$
\begin{align}
\int_0^1f(x)\mathrm{d}x &= \frac2{\pi} \\
\int_0^1f(x)x\,\mathrm{d}x &= \frac4{\pi^2} \\
\int_0^1f(x)x^2\,\mathrm{d}x &= \frac8{\pi^2} \,-\, \frac{16}{\pi^3} \\
\int_0^1f(x)x^3\,\mathrm{d}x &= \frac{12}{\pi^2} \,-\, \frac{96}{\pi^4} \\
\end{align}
$$
となり、
$$
\begin{align}
p(x) &= \left(\frac{13440}{\pi^{4}} \,-\, \frac{3840}{\pi^{3}} \,-\, \frac{240}{\pi^{2}} + \frac{32}{\pi}\right) \\
&+ \left(\frac{-161280}{\pi^{4}} + \frac{43200}{\pi^{3}} + \frac{3360}{\pi^{2}} \,-\, \frac{240}{\pi}\right)x \\
&+ \left(\frac{403200}{\pi^{4}} \,-\, \frac{103680}{\pi^{3}} \,-\, \frac{9360}{\pi^{2}} + \frac{480}{\pi}\right)x^{2} \\
&+ \left(\frac{-268800}{\pi^{4}} + \frac{67200}{\pi^{3}} + \frac{6720}{\pi^{2}} \,-\, \frac{280}{\pi}\right)x^{3} \\
\end{align}
$$
が得られる。
関連キーワード
- ヒルベルト行列
- グラム行列
- 正定値行列