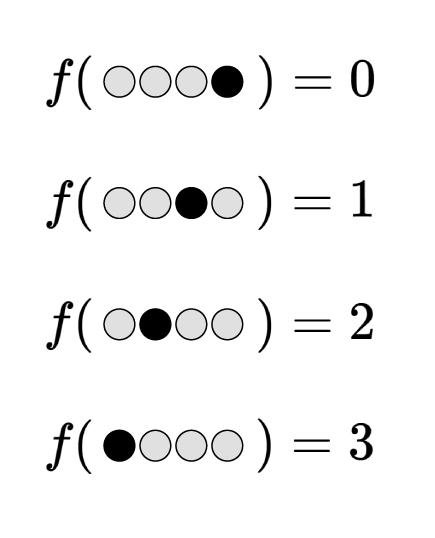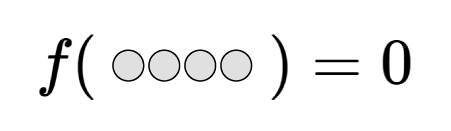この動画で言及されている問題がとても面白かったので、今日はこの問題について考えたいと思う。
この問題の定義については説明しないので、動画を先に見てほしい。動画を見て満足したら、この記事は読まなくても良い。
また、動画の概要欄にある参考記事にも素晴らしい説明が書かれているので、良ければ読んでみて欲しい。
この記事について
この記事では、アリスとボブによる盤面の符号化(エンコーディング)にいくつかのヒューリスティックな仮定をおくと、これが $(\mathbb{Z}/2\mathbb{Z})^n$ と同型になるということを見ていく。
前提:解の存在の可能性について
アリスには 64 通り(=6ビット)の行動が許可されていて、その結果の盤面も異なる 64 通りが存在する。これは、64 通りのマスの位置を伝えるのに十分な情報量である。従って、この問題には解が存在していても矛盾しないと言える。
また、アリスはちょうど 64 通りの行動しか認められていないため、そのうちのどの 2 つの行動の結果の盤面も、異なるマスを指し示していなければならない。
問題の定式化
マスの数を $N$ とする。以降ではマスが右から左に横一列に並んでいるものとして考える。(※冒頭で掲載した動画および参考文献とは逆順のため注意)
アリスは 1 枚のコインを 1 回だけ裏返し、その盤面をボブに見せる。
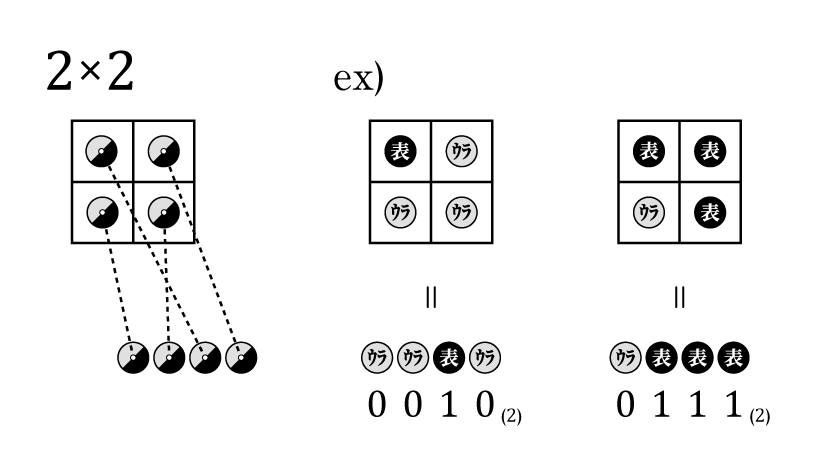
$2^N$ 通り存在する盤面の中からひとつの状態 $S$ がボブに与えられたとき、その値を、マスの位置を示す整数 $n \in \{0,1, \cdots, N-1\}$ に符号化したい。この方法を、以下の条件に従って考える。
ここで、符号化を $f$ で表し、 $n=f(S)$ と書くことにする。
また、 $i$ マス目を裏返す操作を $g_i$ と表し、状態 $S$ の $i$ マス目を裏返した状態を $g_i(S)$ と書くことにする。
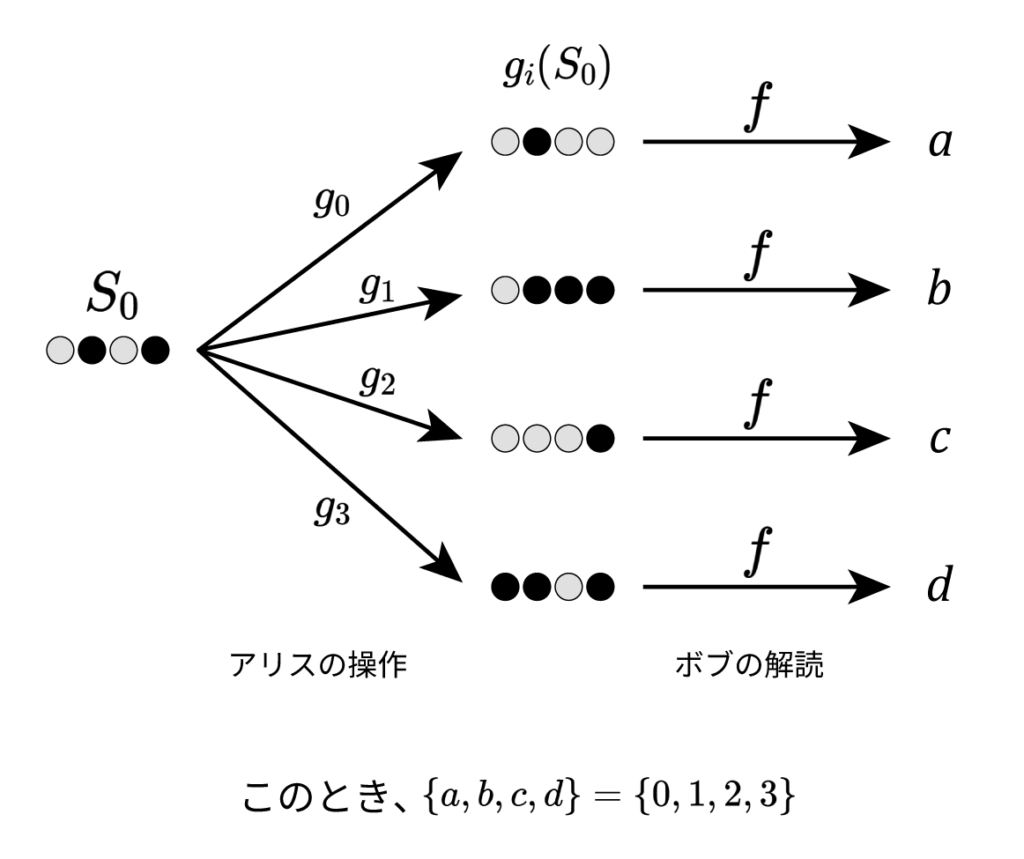
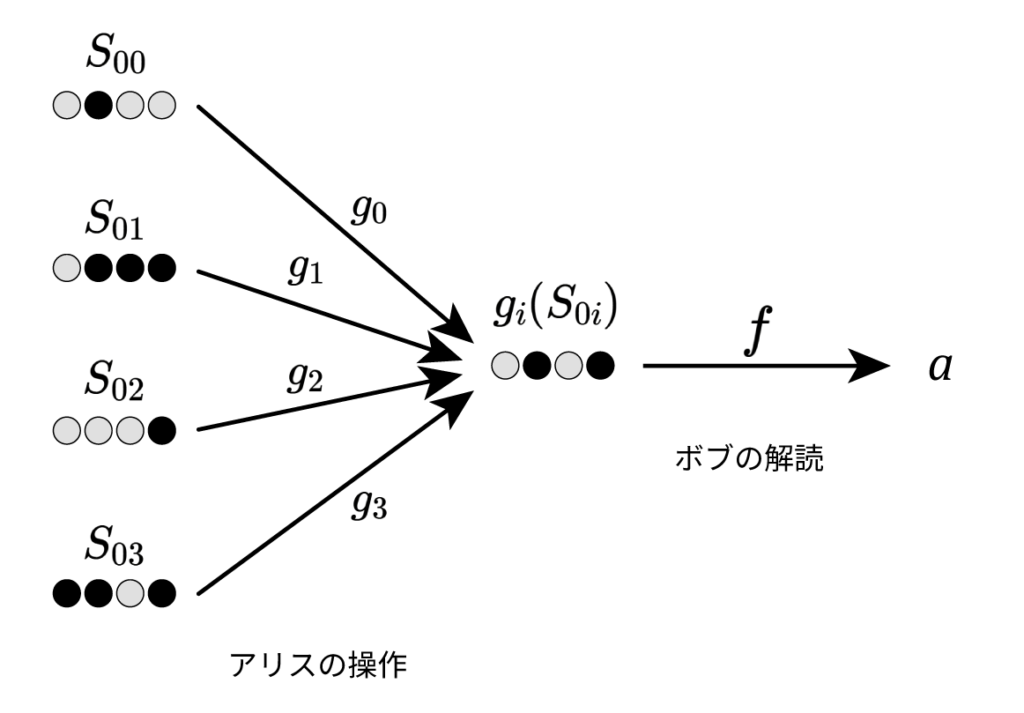
アリスの異なる行動に対して、ボブは異なるマスの位置を指示しなければならない。つまり、看守から与えられた盤面の初期状態 $S_0$ (以降、初期盤面と呼ぶ)がどのようなものだったとしても、その状態からアリスの行動によって遷移できる状態の符号化
$$
\{f(g_0(S_0)),\; f(g_1(S_0)),\; \cdots ,\; f(g_{N-1}(S_0))\}
$$
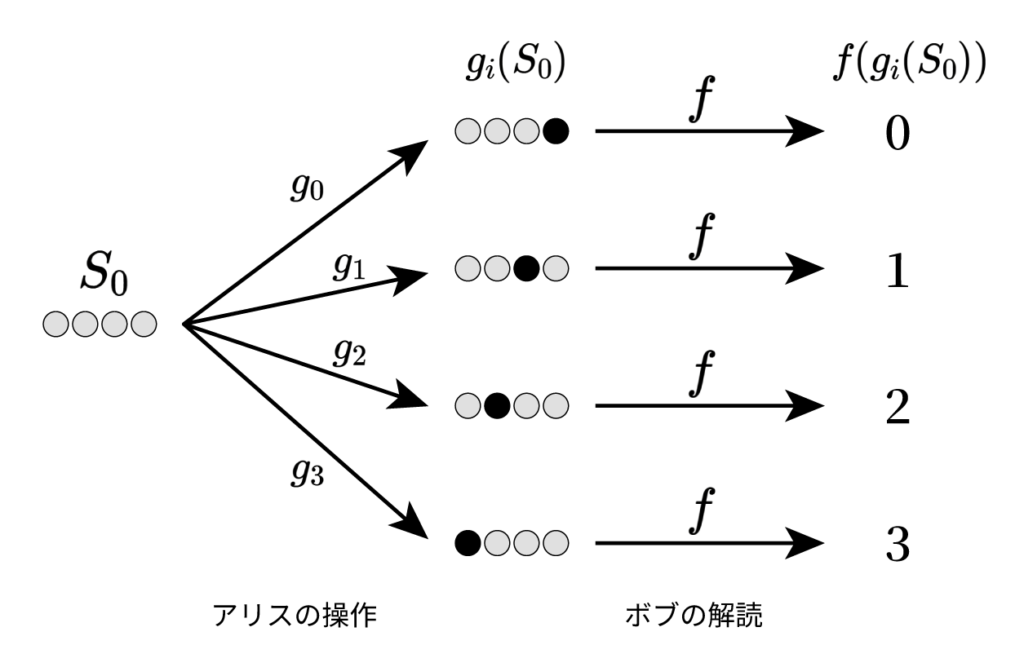
には重複があってはならず、その集合は $\{0,1, \cdots, N-1\}$ と完全に一致していなければならない。たとえば N=4 のとき、
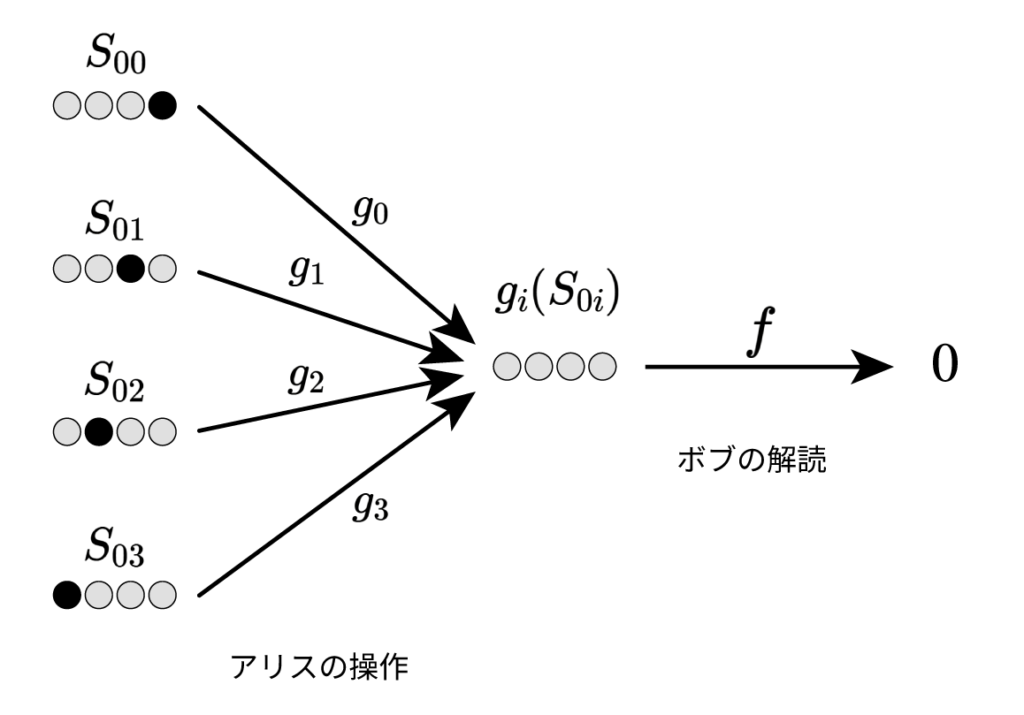
また、異なる初期盤面と異なるアリスの行動から同じ盤面が得られた場合、それは同じ数を指し示していなければならない。
つまり、
$$
g_i(S_{0i}) = g_j(S_{0j}) \implies f(g_i(S_{0i})) = f(g_j(S_{0j}))
$$
でなければならない。(※ 数式で表すと自明であるが。)
説明のため、盤面の表のコインの数を m とし、
$$
m = m(S)
$$
の形で表すことにする。
i. 初期状態で表が m=0 枚のとき
簡単な場合から順番に考えていこう。
看守から与えられた初期状態において表のコインがない場合、つまり $m(S_0)=0$ の場合は簡単で、看守が指定したコインを裏返すのが最も理にかなった行動である。つまり、ボブが盤面を見た時点で $i$ 番目のみが表を向いている場合、ボブは「看守が $i$ 番目のコインを指定した」と理解するものとし、
$$
f(g_i(S_0)) = i
$$
と定める。
正確には、この結果には順列の自由度があり、ボブが区別さえできれば結果の数字を自由に入れ替えても問題ない。しかし、それらには対称性があり、ここでは符号化のうちのひとつを見つければ十分なので、そのようなケースは無視することにする。
ii. 初期状態で表が m=1 枚のとき
このケースでは、唯一の表のコインを裏返した場合、すべて裏向きになる。ボブは、アリスがどれを裏返したかを知ることはできず、符号化の結果は常に同じ値を指していなければならない。その数は何でもよいが、対称性から、これを適当に 0 とする。
ボブはすべてのコインが裏向きだった場合、「看守は 0 番目のコインを指定した」と判断する。
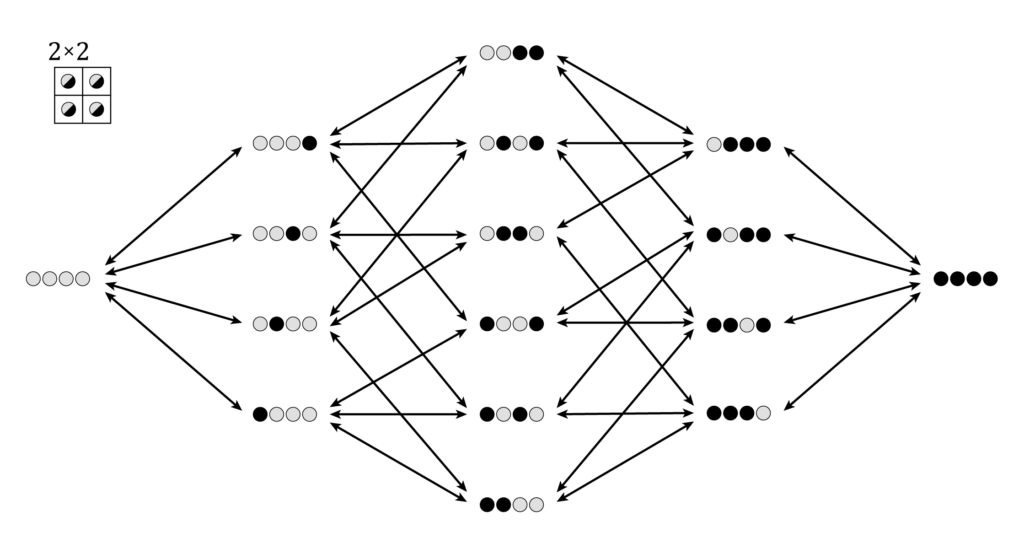
一方で、アリスが裏向きのコインを裏返すと、表向きのコインは 2 枚になる。例として N=4 の場合を考えてみる。
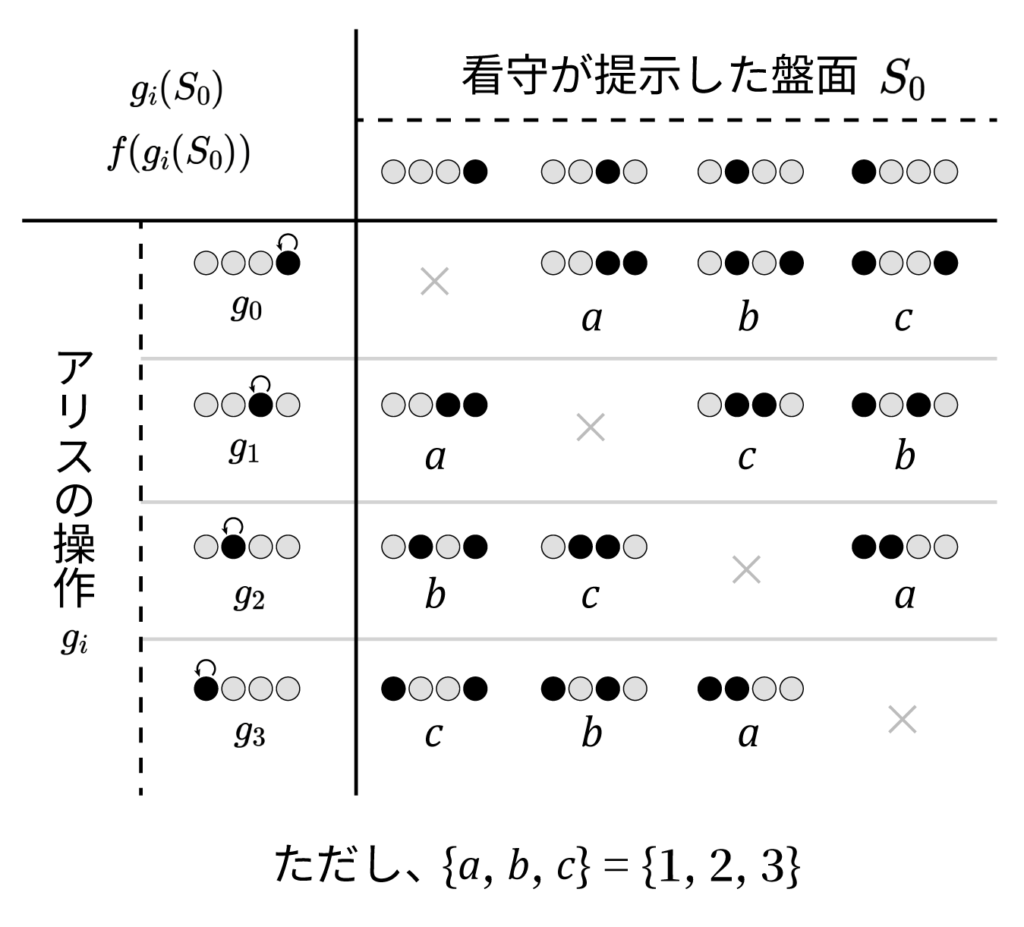
このときボブが受け取る盤面は ${}_4 \mathrm{C}_2 = 6$ 通り存在する。そして、ボブはそれを見て 1~3 のいずれかを答えなければならない。ここで、
- 同じ盤面は同じ数字に符号化される
- 同じ列に同じ数字が入ってはいけない
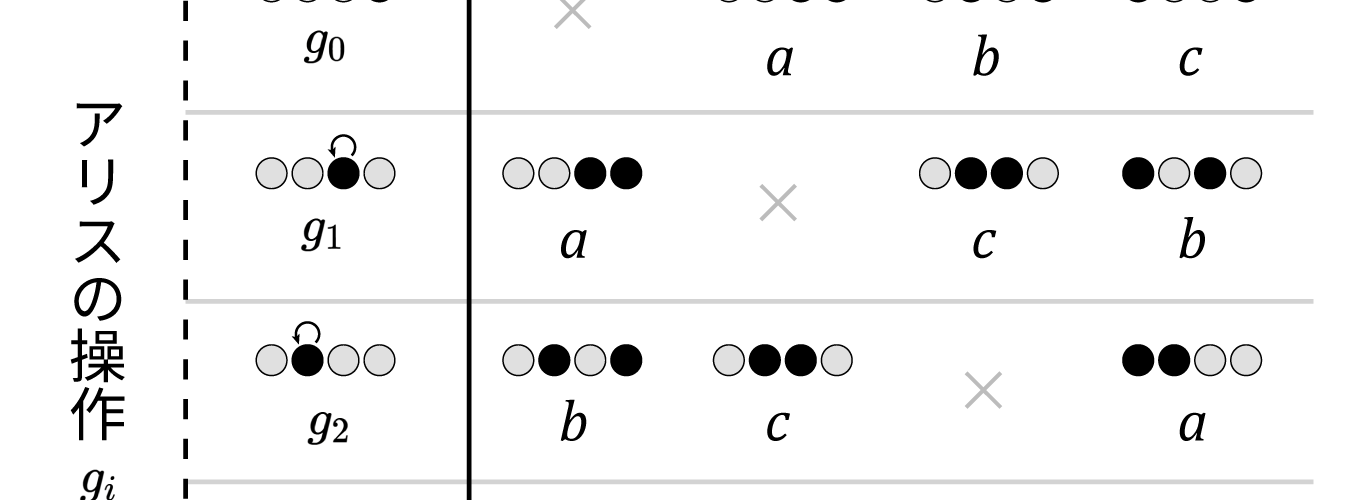
という条件に従ってテーブルを埋めると、上記のようになる。そして、これは二項演算のように見える。
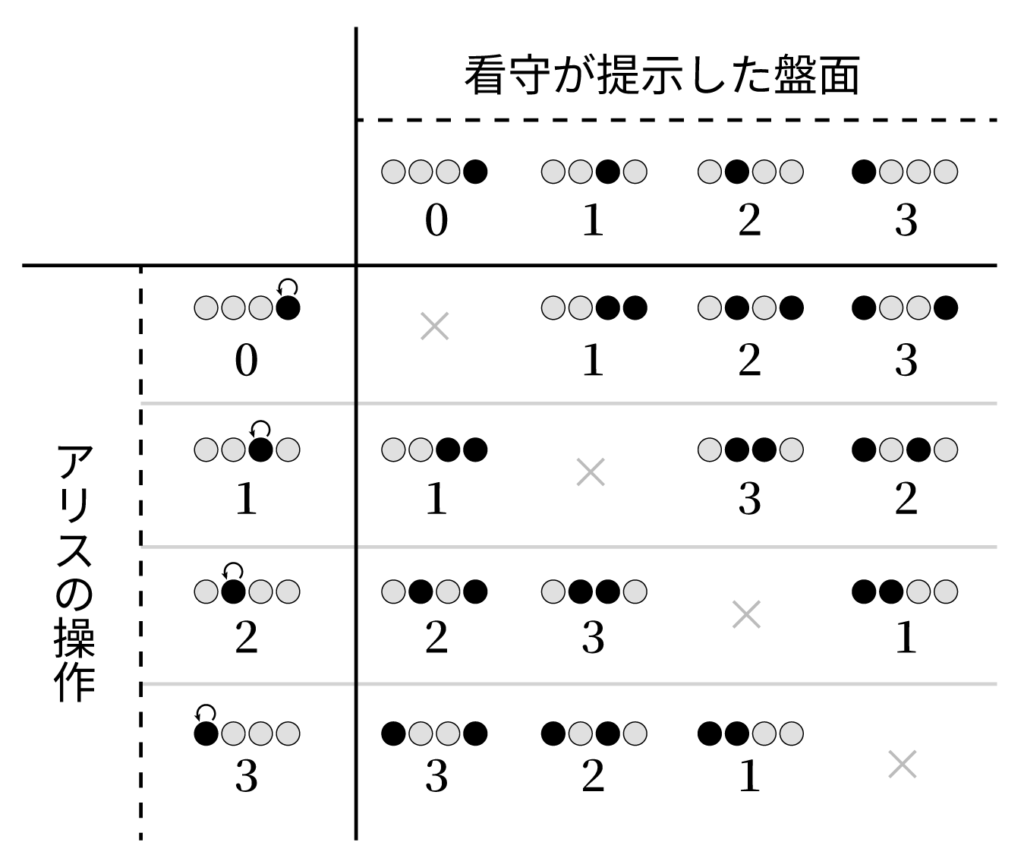
ボブが区別さえできれば良いという意味で a, b, c には対称性があるため、0 以外の残りの数字を適当に当てはめてみる。さらに「看守が提示した盤面」「アリスの操作」にも適当な連番を付けると、以下のような表ができる。「×」となっている箇所は今は考えていないため、何が入ってもよい。
これは mod 4 での足し算 $(\mathbb{Z}/4\mathbb{Z}, +)$ のようにも見えるが、完全には一致していない。
$$
\begin{array}{c|cccc}
\;+_{\mathbb{Z}/4\mathbb{Z}} & 0 & 1 & 2 & 3 \\
\hline
0 & 0 & 1 & 2 & 3 \\
1 & 1 & 2 & 3 & 0 \\
2 & 2 & 3 & 0 & 1 \\
3 & 3 & 0 & 1 & 2 \\
\end{array}
$$
mod 4 での減算と見なしてはどうだろうか? しかし、これとも一致しない。
$$
\begin{array}{c|cccc}
\;-_{\mathbb{Z}/4\mathbb{Z}} & 0 & 1 & 2 & 3 \\
\hline
0 & 0 & 1 & 2 & 3 \\
1 & 3 & 0 & 1 & 2 \\
2 & 2 & 3 & 0 & 1 \\
3 & 1 & 2 & 3 & 0 \\
\end{array}
$$
ところで、先ほどの謎の演算を全域的にして正確な二項演算にしたい。「×」となっている箇所は何が入ってもよいので、その箇所に 0 を埋めてみる。すると、これは以下のようになる。
$$
\begin{array}{c|cccc}
\ast & 0 & 1 & 2 & 3 \\
\hline
0 & 0 & 1 & 2 & 3 \\
1 & 1 & 0 & 3 & 2 \\
2 & 2 & 3 & 0 & 1 \\
3 & 3 & 2 & 1 & 0 \\
\end{array}
$$
N=4 の場合はボブにこの表を伝えればよいが、N=64 の場合に 64×64 の表を伝えるのは骨が折れる。N=64 の場合でも、この表を系統的に構成することはできるだろうか。あるいは、この謎の演算を数学的に説明できるだろうか。
有限アーベル群であるための必要条件
先ほどの積表(乗積表)は、対角成分に 0 を埋めたことで、N の値によらず、以下のような条件を満たしている。
- どの行・列にも同じ数が存在しない(可除性;群の意味での逆元の存在の可能性を示唆)
- 対角線を対称の軸として線対称になっている(交換法則)
- 単位元 0 が存在する(適当な仮定により)
これは、先ほどの積表によって表される二項演算が有限アーベル群であることと矛盾しない。
しかし、結合律を満たすとは限らない。実際、N=8 の場合には条件を満たすような結合的でない積表が存在する。
$$
\begin{array}{c|cccc}
\ast & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
\hline
0 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\
1 & 1 & 0 & 3 & 2 & 5 & 4 & 7 & 6 \\
2 & 2 & 3 & 0 & 1 & 6 & 7 & 4 & 5 \\
3 & 3 & 2 & 1 & 0 & 7 & 6 & 5 & 4 \\
4 & 4 & 5 & 6 & 7 & 0 & 1 & 3 & 2 \\
5 & 5 & 4 & 7 & 6 & 1 & 0 & 2 & 3 \\
6 & 6 & 7 & 4 & 5 & 3 & 2 & 0 & 1 \\
7 & 7 & 6 & 5 & 4 & 2 & 3 & 1 & 0 \\
\end{array}
$$
この場合、具体的に、
$$
(2\ast4)\ast4=3\ne2=2\ast(4\ast4)
$$
となってしまう。
しかし、そうだとしても、もし結合律を満たすような演算がひとつでも存在すれば、それは $f$ の候補となり、(m=1 のケースにおいて)表題のパズルは解決したことになる。
そのような有限アーベル群 $G$ は位数 $N=64$ においても存在するだろうか。
これを確認するために、この二項演算が有限アーベル群であると仮定し、これを G と置く。(この時点ではまだそのような G が存在するかどうかはわからない。) $G$ に関する追加条件で、対角成分が 0 になるというものがあった。つまり、
- すべての $G$ の元は $a\ast a=0$ を満たす
- 従って、すべての元の位数は 2 の約数である
- 従って、すべての元の位数は 1 または 2 である
- 従って、位数が 3 以上の元は存在しない
- 従って、位数が 3 以上の巡回部分群は存在しない
- 従って、この群を巡回群の直積に分解したとき、それらのいずれも位数 2 である
従って、もし $G$ が存在するならば、
$$
G=(\mathbb{Z}/2\mathbb{Z})\times(\mathbb{Z}/2\mathbb{Z})\times\cdots\times(\mathbb{Z}/2\mathbb{Z})
$$
であるか、またはこれに同型でなければならない。
このような群は、$G$ の位数 N が 2 の累乗数であるときにのみ存在して、そのとき、最初に課したすべての条件を満たす。この演算は、
$$
\mathrm{XOR}
$$
と同一視できて、また、これは有限体 $\mathbb{F}_N$ の加法群でもある。
以下では結合則が成り立つことを仮定する。また、記法の簡潔さのため、演算 ${}\ast{}$ を XOR のように扱う。
iii. 初期状態で表が m≧2 枚の場合
最後に、上記の議論を拡張して、 $m\ge2$ の場合にも適用できるかどうかを考える。
表のコインが $m(S) \ge 2$ 個の盤面 $S$ の符号化を系統的に定義したい。たとえば、$G$ 上の演算 (XOR) を用いて、以下のように $m(S)$ 個の数の XOR に分解する。
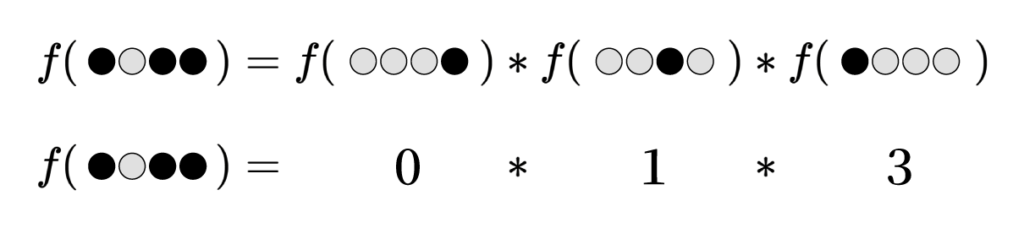
ただし、ここまでの議論と矛盾しないように、i 番目のコインのみが表であるような盤面の符号化は i であるものとする。たとえば、 N=4 のとき、
である。このようにして、任意の盤面の符号化を定義することができる。このように構成した符号は、 $f$ が満たすべき条件を満たすだろうか。
アリスが構成できる N 個の盤面は異なる数字を伝えられるか?
看守が与えた盤面 $S_0$ に対して、アリスが i 番目のコインを裏返した場合、盤面の符号化がどのようになるかを考える。
ここで、i 番目のコインを裏から表に裏返す操作は、i を掛けることで表現できる。
1. 初期盤面の i 番目のコインが裏だった場合
符号化の結果は
$$
f(g_i(S_0)) = i \ast f(S_0)
$$
となる。
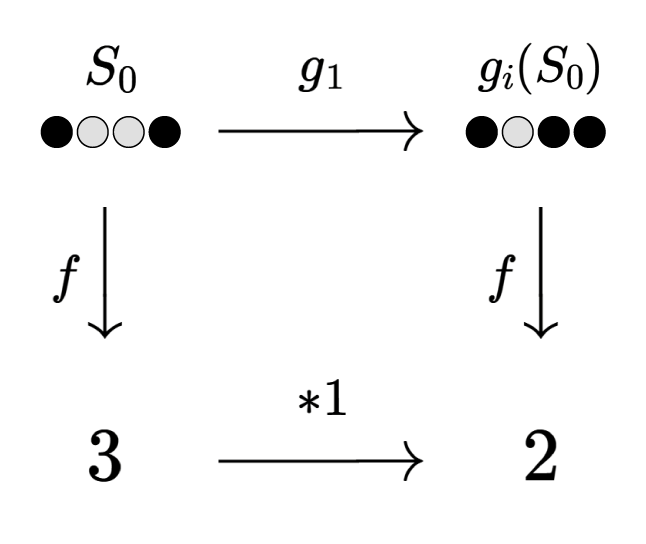
$$
\begin{CD}
S_0 @>g_i>> g_i(S_0) \\
@V f VV @V f VV \\
f(S_0) @> {}\ast i >> i \ast f(S_0)
\end{CD}
$$
たとえば、$N=4,\, i=1$ のとき
のようになる。
2. 初期盤面の i 番目のコインが表だった場合
$$
i \ast f(g_i(S_0)) = f(S_0)
$$
であり、両辺に $i$ を掛けて
$$
f(g_i(S_0)) = i \ast f(S_0)
$$
が得られる。
$$
\begin{CD}
S_0 @>g_i>> g_i(S_0) \\
@V f VV @V f VV \\
i \ast f(g_i(S_0)) @< {}\ast i << f(g_i(S_0))
\end{CD}
$$
以上から、いずれの場合でもボブが受け取る符号は $i \ast f(S_0)$ となることが分かった。 $i$ が異なるとき、この符号化も異なる数になるため、アリスは常に N 通りの異なる符号をボブに伝えることができる。
アリスは何を裏返せばよいか?
伝えたい数 n(つまり、看守が指示したマスの位置を示す整数)に対して、f の定義より
$$
n = f(g_i(S_0)) = i \ast f(S_0)
$$
であるから、両辺に初期盤面の符号化 $f(S_0)$ を掛けて
$$
i = n \ast f(S_0)
$$
となるような位置 $i$ のコインを裏返せばよい。
より具体的な計算方法は動画の通りである。
ボブは何と答えればよいか?
f の定義の通り、受け取った盤面 $S$ に対して、
$$
f(S)
$$
と答えればよい。
より具体的な計算方法は動画の通りである。
今後の課題
- m=1 の場合における、結合律を仮定しない場合の可能な積表の一覧と、同型な積表の個数
- 妥当な符号化は、 (N!)^2 通りの同値な置換を除いて、唯一のものしか存在しないのかどうか