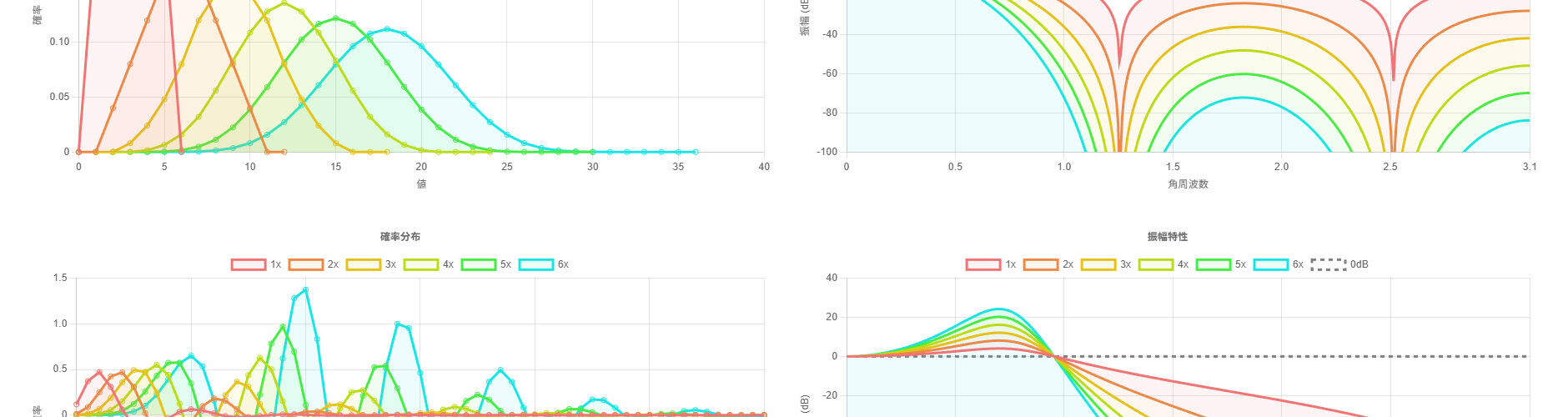
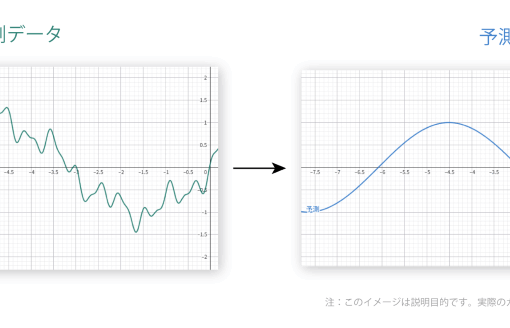
確率質量関数とインパルス応答の類似性
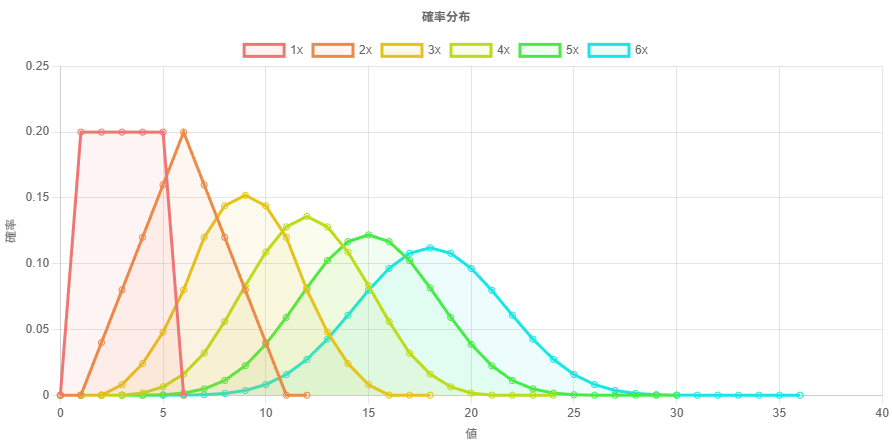
ここで、ブラーを複数回掛ける話に戻る。画像に対して複数回ボックスブラーを掛けるケースを考える。このときのインパルス応答は、カーネル同士を畳み込むことで計算できる。ボックスブラーのカーネルを1次元分だけ取り出して、離散確率分布の確率質量関数とみなすと、六面サイコロのケースと(ピクセルのオフセットの差を除いて)一致することがわかる。(※ボックスブラーは次元に分離可能)
$$
y[n] = \frac{1}{2N+1}\sum_{k=-N}^{N}{x[n+k]}
$$
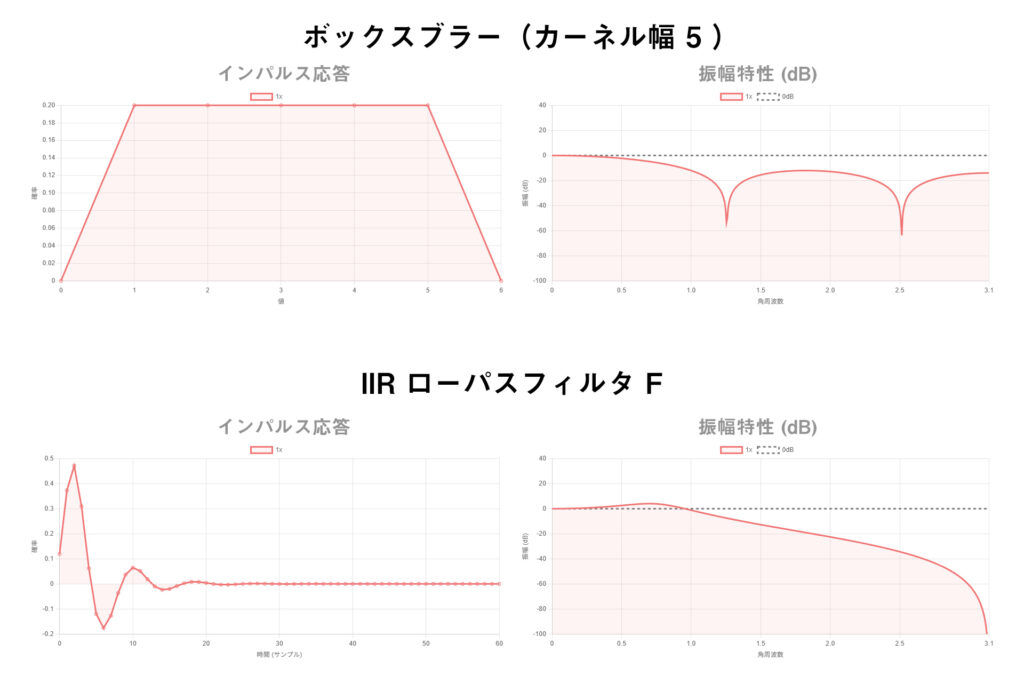
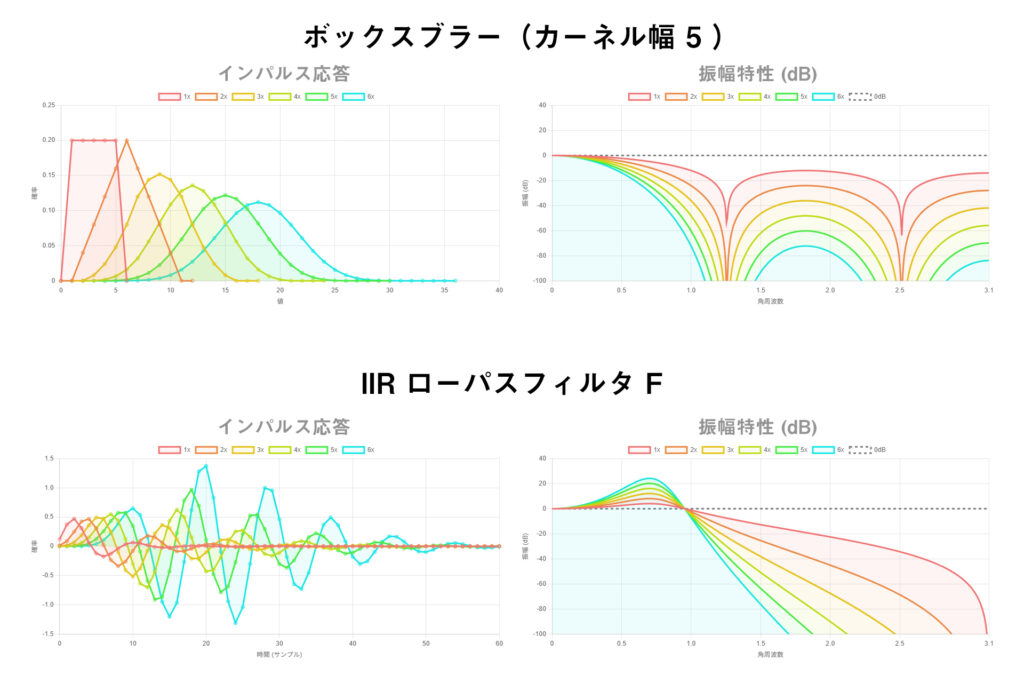
カーネル幅 5 (ぼかし半径 N=2) の場合のインパルス応答をプロットしてみると、サイコロのケースとほとんど同様になっていることが分かる。
このように、ボックスブラーを繰り返し実行することでガウスぼかしに近付く原理を、中心極限定理の視点で考えることができる。
IIR ローパスフィルタ
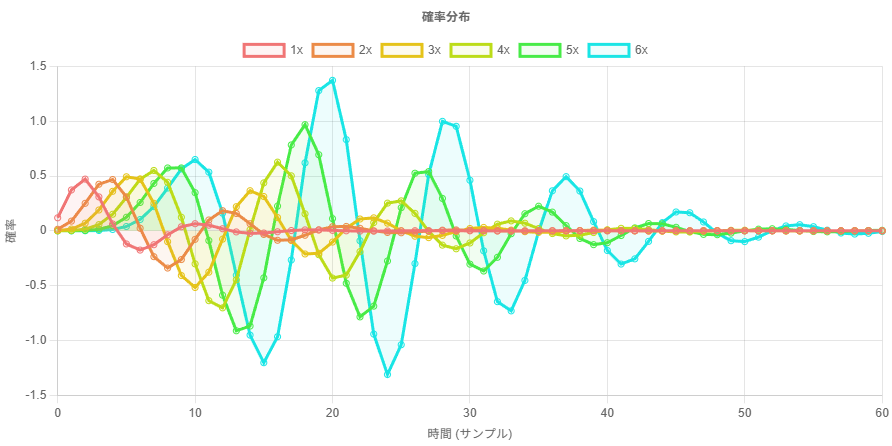
ここで、他の LTI (線形時不変)フィルタではどうなるのかが気になってくる。他のインパルス応答でも、畳み込みを繰り返すとガウス関数に収束するのだろうか? 試しに適当な設計の IIR ローパスフィルタ F を考えてみる。
$$
y[n] = b_0 x[n] + b_1 x[n-1] + b_2 x[n-2] \,-\, a_1 y[n-1] \,-\, a_2 y[n-2]
$$
これを繰り返し畳み込むと、収束せず発散してしまう。
このように発散してしまうのは、一体なぜだろうか?
振幅特性と畳み込み
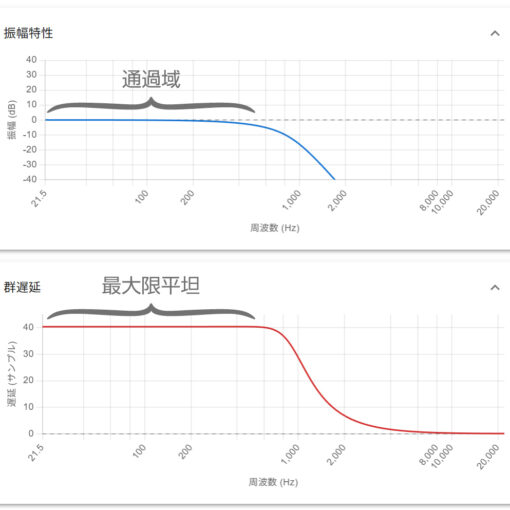
ここで、ボックスブラーと IIR ローパスフィルタ F の振幅特性を見てみると答えが明確になる。
振幅特性は上記のようになっている。どちらもローパス的な性質を持っているフィルタだということがわかる。
ここで、自己畳込みは周波数軸における冪乗に相当するため、フィルタ n 回の重ね掛けに対して dB は n 倍になる。
$$
\begin{align}
G(\omega)
&= 20 \log_{10} \left| H(\omega) \right| \\[12pt]
G_n(\omega)
&= 20 \log_{10} \left| H(\omega)^n \right| \\[5pt]
&= 20 \log_{10} \left| H(\omega) \right|^n \\[5pt]
&= 20 n \log_{10} \left| H(\omega) \right|
\end{align}
$$
※ 補足: $H(\omega)$ と書いた場合は $H(e^{j\omega})$ を表すものとする
さて、フィルタを重ねがけするとどうなるかをグラフで表してみる。
ボックスブラーでは、振幅特性
$$
\left| H\left( \omega \right) \right|^n
$$
がなめらかな形に収束している。(※注意 : 正確には、スケーリングを補正した
$$
\left| H\left( \frac{\omega}{\sqrt{n}} \right) \right|^n
$$
が収束する。)
サイドローブもいずれは $-\infty$ dB に収束するだろう。
一方で、IIR フィルタ F では共振があり、 $|H(\omega)|>0$ の部分が発散していることがわかる。
ガウスぼかしを近似できるための必要条件(予想)
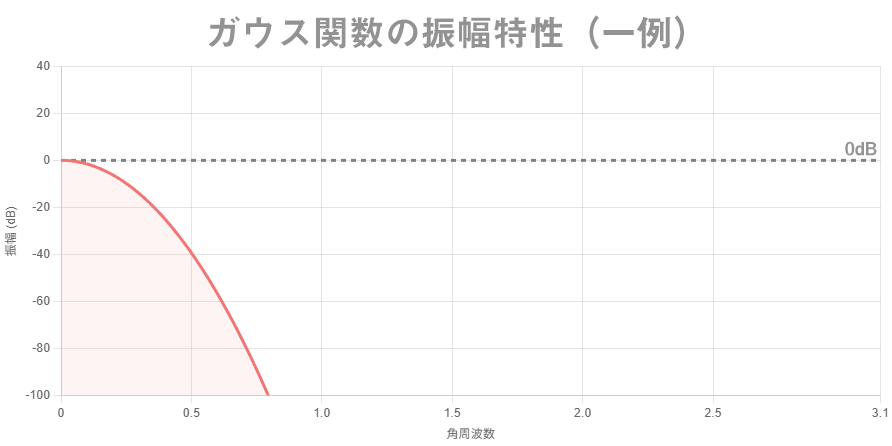
実ガウス関数のフーリエ変換はガウス関数になり、 $\omega=0$ を中心とする単峰型の振幅特性になるはずなので、線形時不変フィルタの重ね掛けでガウスぼかしを近似できるためには、 $\omega\ne 0$ で振幅特性が $|H(\omega)| < 1$ でなければならないという予想が立つ。
次の記事では、中心極限定理の定義について再確認し、この予想の妥当性について検証する。