結論に向かう前に、今回は中心極限定理の可視化ツールを紹介します。
このツールでは、確率変数の和が正規分布に収束していく様子や、「正規分布の分散が大きくなると、そのフーリエ変換の分散が小さくなること」などをインタラクティブに確認できます。
1. 確率質量関数
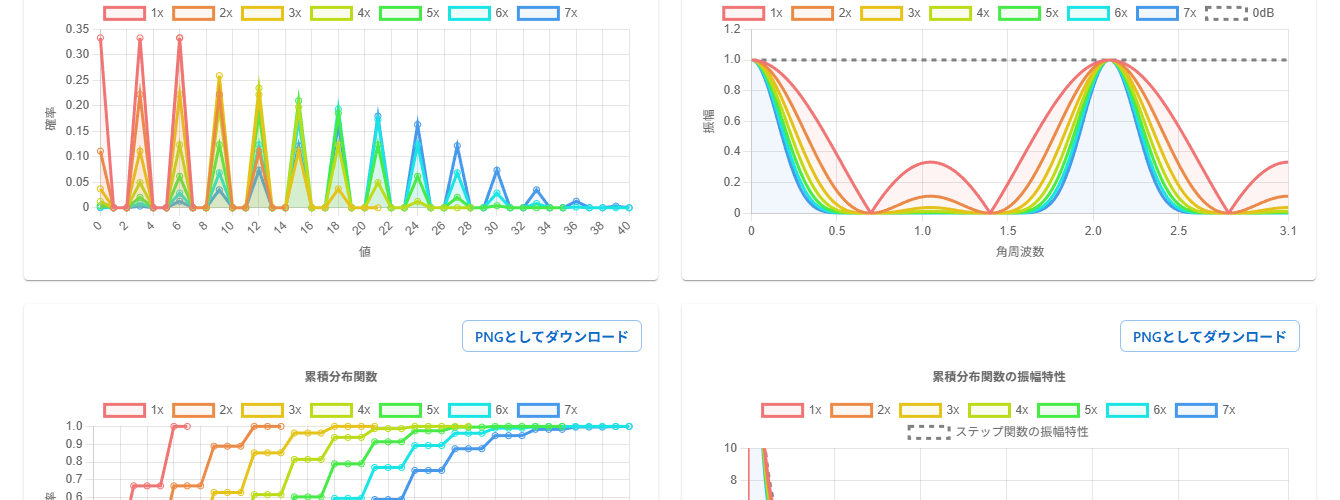
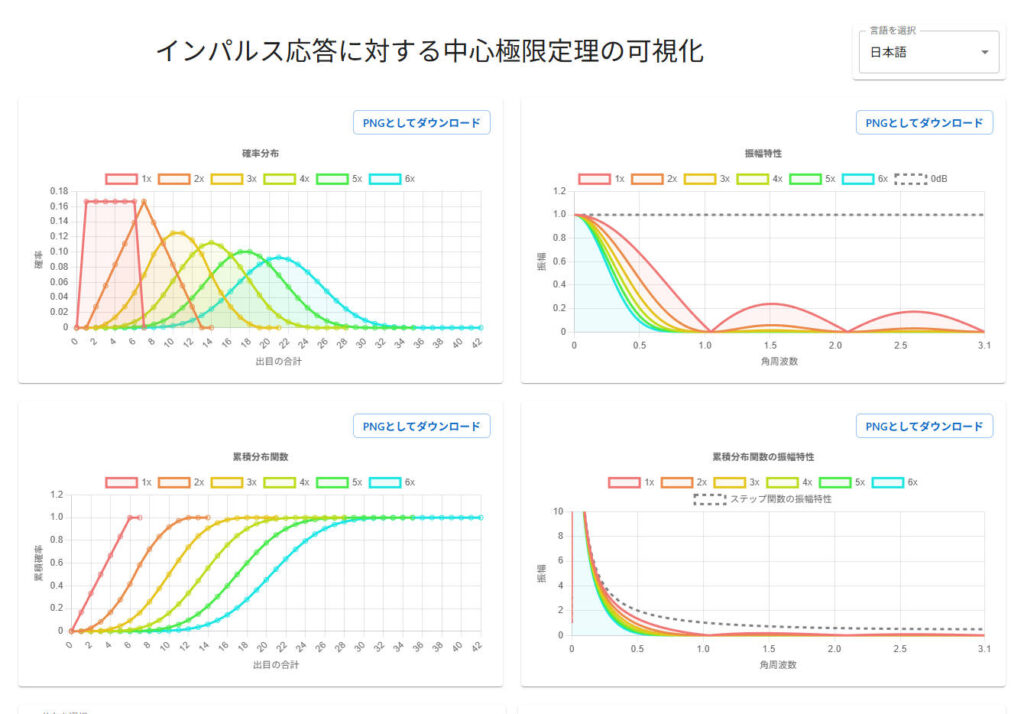
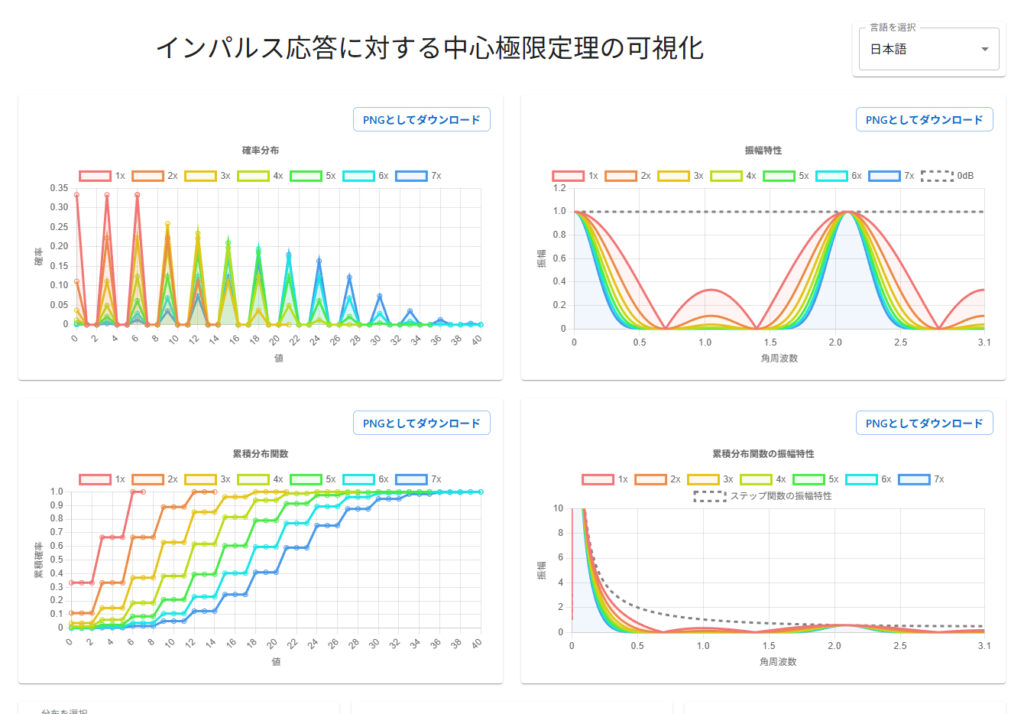
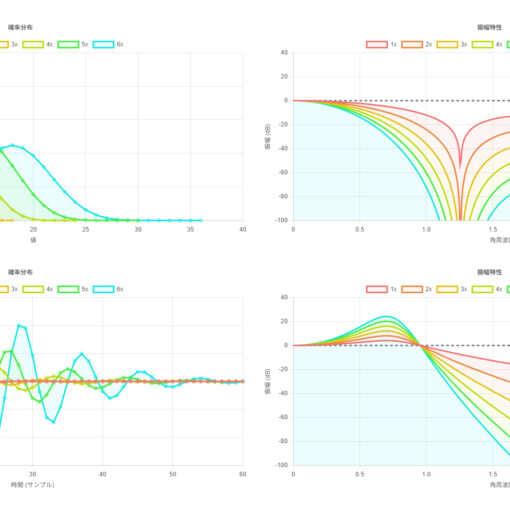
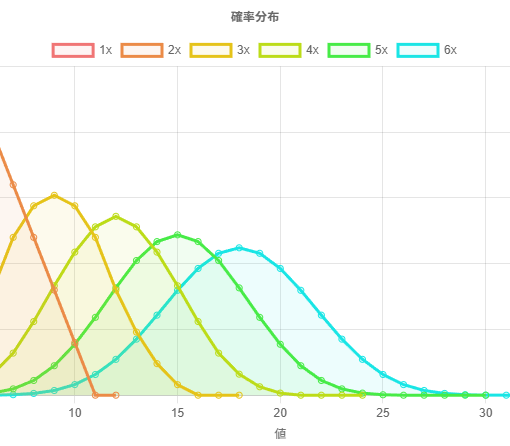
左上に表示されているのは確率質量関数、またはインパルス応答で、実数です。ドロップダウンリストで分布を選択することが出来ます。
$$
h[n]=P(X=n) \quad (n\in \mathbb{Z})
$$
2. 振幅特性
右上に表示されているのは振幅特性 $|H(\omega)|$ です。
フーリエ変換を使用した定義
$$
H(\omega)
= \sum_{n=-\infty}^{\infty} e^{-i\omega n}\,h[n]
$$
特性関数を使用した定義
$$
\varphi_X(\omega)
= \sum_{n=-\infty}^{\infty} e^{i\omega n}\,P(X=n)
$$
指数の肩の符号が異なりますが、どちらも絶対値を取ると同じ値になります。
3. 累積分布関数の表示
また、これは次回の記事のネタバレなのですが、画面の下半分に、累積分布関数とそのフーリエ変換も表示できるため、「確率質量関数がガウス型にならなくても、累積分布関数は正規分布のそれに収束することがある」、ということなども確認できます。
画面の拡大・縮小にはブラウザの機能を使用してください。
また、スマートフォンでも閲覧できますが、基本的には PC での閲覧をおすすめします。スマートフォンで見る場合は、PC 版表示にするか、ズーム機能で縮小してください。
次回へのリンク：
