どんなブラーでも繰り返し実行することでガウスぼかしを近似できるのか？（連載・インパルス応答と中心極限定理 1）

Wikipedia の「ガウシアンぼかし」のページには「ぼかし処理を繰り返し適用することでガウスぼかしを近似する結果を得ることもできる」と記載されていて、これは確かに成立する。

たとえば、ボックスブラーを考える。

$$
y[m,n]
=
\frac{1}{(2r+1)^2}
\sum_{i=-r}^{r}
\sum_{j=-r}^{r}
x[m+i,\,n+j]
$$

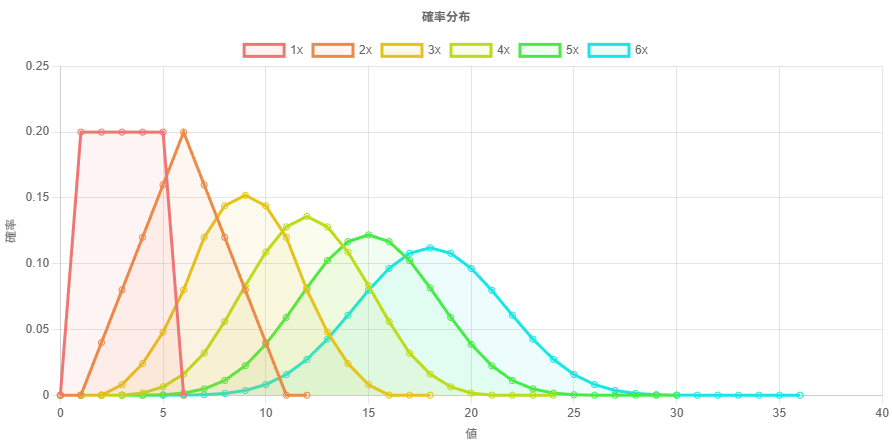
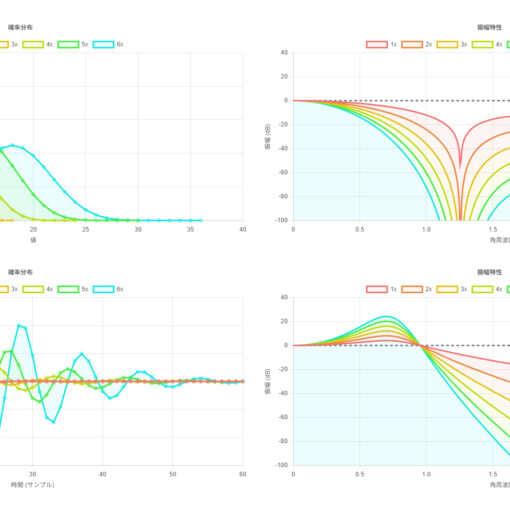
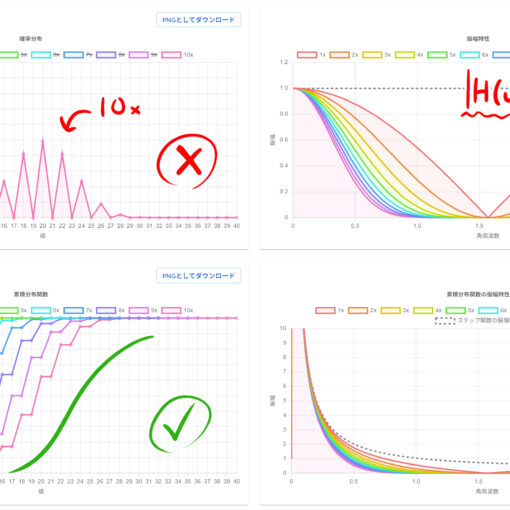
以下の画像を見ると、1 回のボックスブラーではエッジが目立っているが、繰り返し何度もボックスブラーを掛けることで、ガウスぼかしとある程度似たような結果を得ることができている。

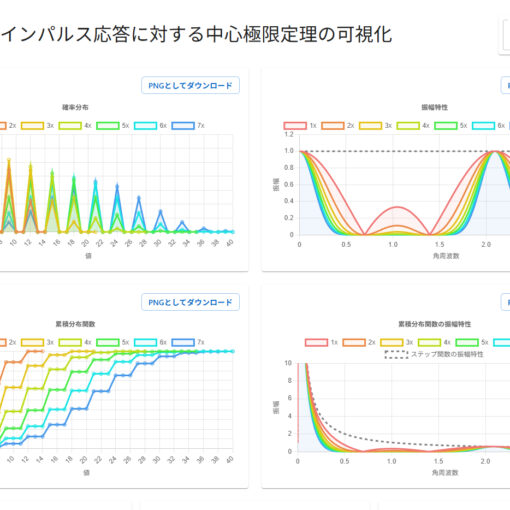
一次元のグラフで確認してみると、確かにボックスブラーを何度も掛けると、ガウス関数（正規分布の確率密度関数）のような形に近付いていることが確認できる。

しかし、任意の LTI フィルタに対しても、それを重ねがけすることで、ガウスぼかしを近似することができるのだろうか？答えは「いいえ」であり、4 ピクセル横または縦にずらして重ねるフィルタを考えると、これは重ねがけしてもガウスぼかしにならない。

$$
y[m,n]
=
\frac{1}{4}
\left(
x[m-2,\,n-2]
+
x[m-2,\,n+2]
+
x[m+2,\,n-2]
+
x[m+2,\,n+2]
\right)
$$

（※ ここではコムフィルタとの類似性から、仮にくし状ブラーと呼ぶことにする。）

では、中心極限定理はどんなフィルタに対して成立するのだろうか？ガウスぼかしを近似できる条件とは異なるのか？ブラーに対して求められる条件とどのように関係があるのか？これを調べていくことにする。