問題提起
Wikipedia のベッセルフィルタの項目には次のように記載されている。
ベッセルフィルタはクロスオーバー（高音域と低音域などの分離を行う回路）によく使われる。
この記述を見ると、デジタルマスタリングにおけるマルチバンドコンプレッサーなどで用いられるクロスオーバーフィルタでは、ベッセルフィルタを用いることが最適であるかのように感じられる。
（※画像はデジタルマスタリングツールのイメージです。この記事は特定の製品とは無関係です。）
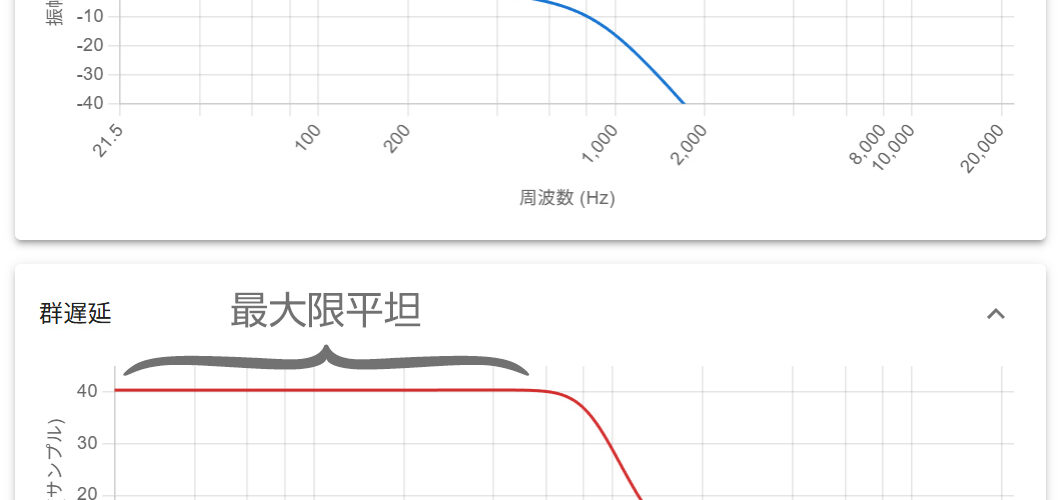
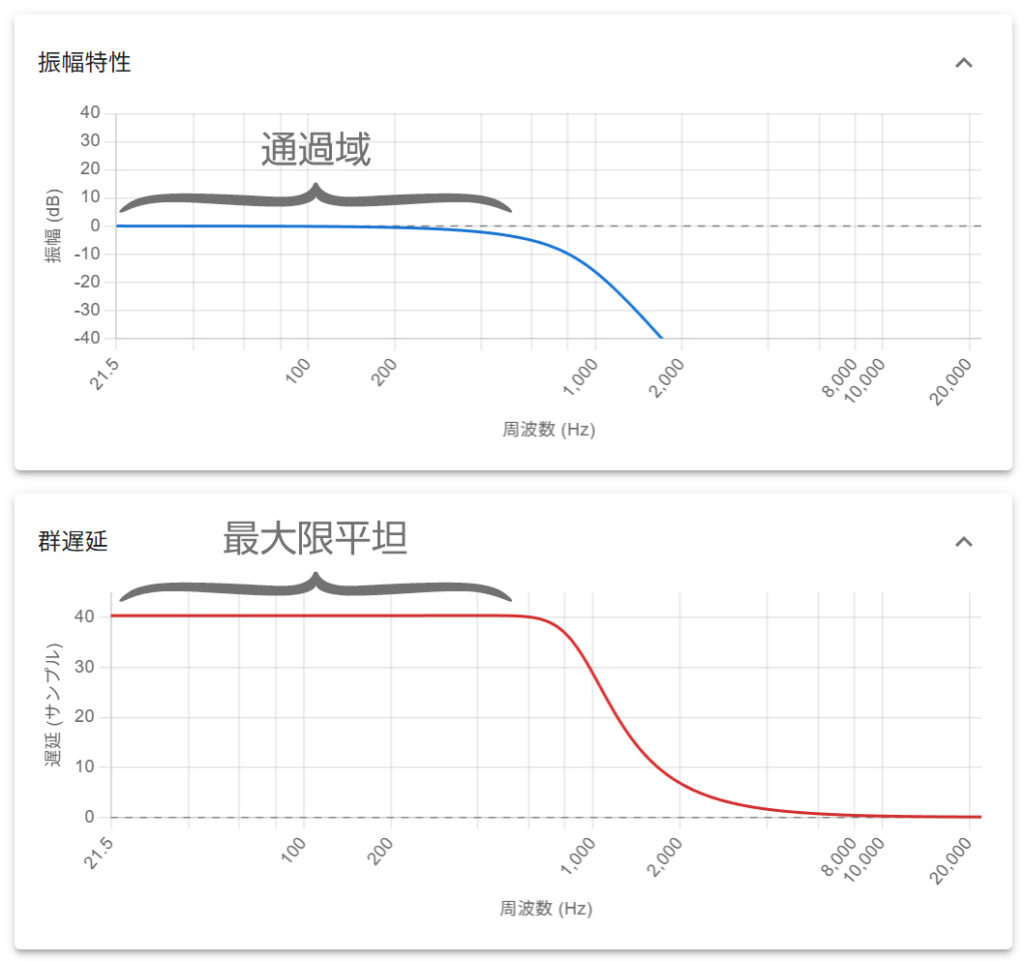
確かに、ベッセルフィルタは低域で群遅延が最大限平坦であり、つまり、IIR でありながら、フィルタを通して線形位相に近い低域成分を取り出すことができる。これにより、FIR/FFT を使用した場合と比べて計算量や遅延時間を抑えることができる。
ベッセルフィルタの HPF
しかし、高域側で群遅延が最大限平坦になるようなベッセルフィルタの HPF をデジタルフィルタで実装することは難しい。たとえば、一つの方法として、LPF フィルタの伝達関数 $H(s)$ から HPF の伝達関数 $H(\omega_c^2/s)$ を構成し、それを双一次変換でデジタルフィルタに変換する、という方法を用いることが出来る。たとえば、
$$
H_\mathrm{LPF}(s)=\frac{15}{s^3+6s^2+15s+15}
$$
のとき、
$$
\begin{align}
H_\mathrm{HPF}(s)
&= H_\mathrm{LPF}\left(\frac{\omega_c^2}{s}\right) \\[5pt]
&= H_\mathrm{LPF}\left(\frac{1}{s}\right)\\[5pt]
&= \frac{15s^3}{1+6s+15s^2+15s^3}\\[5pt]
&= \frac{15s^3}{15s^3+15s^2+6s+1}\\[5pt]
\end{align}
$$
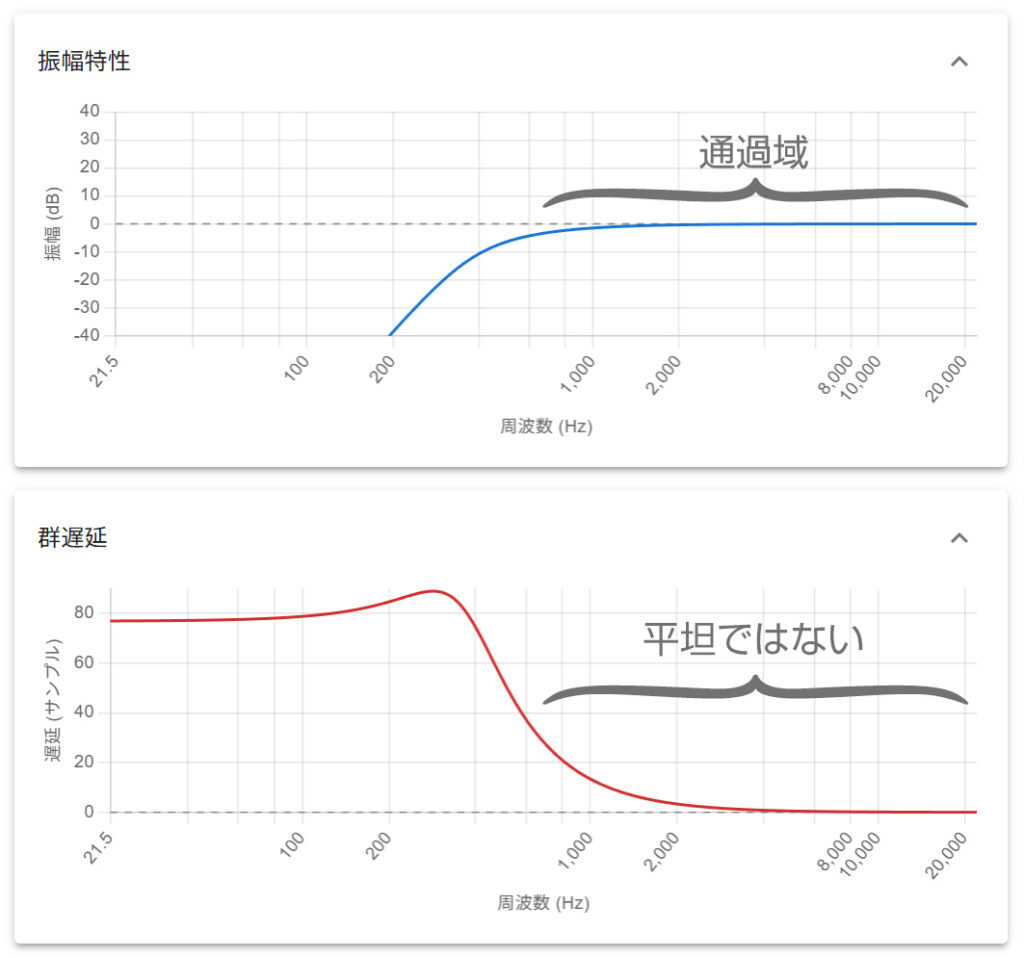
である。しかし、この方法では、高域側の群遅延が平坦にならない。
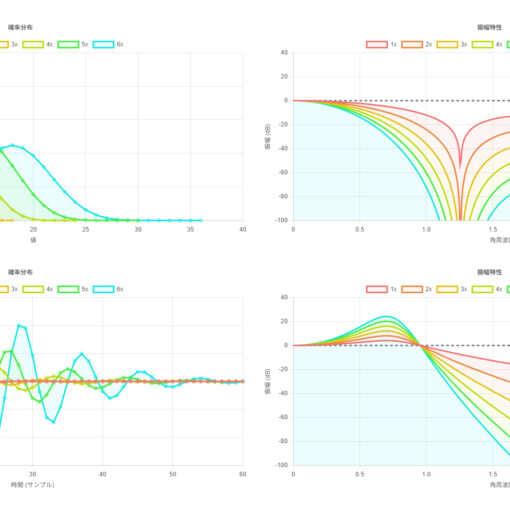
以下に、このアナログプロトタイプをデジタルフィルタに変換した場合の特性の一例を示す。
遅延時間の補償
また、遅延時間補償の問題もある。
仮に高域側で群遅延が最大限平坦な HPF を構成できたとする。しかし、この場合、マルチバンドコンプレッサーの高域バンドと低域バンドが干渉しないように、通過域での遅延サンプル数を一致させる必要がある。このためには、LPF の $\omega=0$ の周辺での群遅延と、 HPF の $\omega=\pi$ の周辺での群遅延が一致するように、定数時間の遅延を追加しなければならない。
しかし、この遅延時間は整数サンプルになるとは限らず、そのような非整数時間の遅延フィルタを高品質に構成するためにはまた別のフィルタが必要になってしまう。
実装例： Thiran フィルタ
thiran – Thiran 近似に基づいて非整数遅延フィルターを作成 – MATLAB
代替：Linkwitz-Riley フィルタ
そこで、代替として Linkwitz-Riley フィルタを用いることができる。
マルチバンド（オーディオクロスオーバー）処理を実現するフィルタ（Butterworth, Linkwitz-Riley）のPython実装（2バンド）
このフィルタは、高域側と低域側で位相特性および群遅延特性が一致し、干渉が生じない。このため、マルチバンドコンプレッサーに適している。
ただし、群遅延は最大限平坦ではないため、そのような特性が必要な場合には適さない。
Linkwitz-Riley フィルタの具体的な解説はリンク先に譲る。
高周波側で群遅延が最大限平坦なデジタルハイパスフィルタは設計できないのか？
原理上できないとは考えにくいが、そのためにはさらなる専門的な知識が必要で、私の理解を超えているため、今後の課題としたい。
ただし、少なくともタイトルにあるように、ベッセル型ローパスフィルタのアナログプロトタイプから構成することは難しいと言える。
備考
他にも、線形位相を重視した FIR フィルタによるクロスオーバーなどがマルチバンドコンプレッサーに用いられる場合もある。
また、ベッセルフィルタまたはその発展形を用いたクロスオーバーも原理的には可能であり、全く存在しないということを主張するわけではない。
参考文献
[1] ベッセルフィルタ – Wikipedia
https://ja.wikipedia.org/wiki/%E3%83%99%E3%83%83%E3%82%BB%E3%83%AB%E3%83%95%E3%82%A3%E3%83%AB%E3%82%BF
[2] マルチバンド（オーディオクロスオーバー）処理を実現するフィルタ（Butterworth, Linkwitz-Riley）のPython実装（2バンド）
https://www.wizard-notes.com/entry/python/audio-crossover-filter-2-band
[3] 験震時報 第56巻 pp.17-34 ベッセルディジタルフィルタの自動設計について
https://www.jma.go.jp/jma/kishou/books/kenshin/kenshin5.html
[4] thiran – Thiran 近似に基づいて非整数遅延フィルターを作成 – MATLAB
https://jp.mathworks.com/help/control/ref/thiran.html
