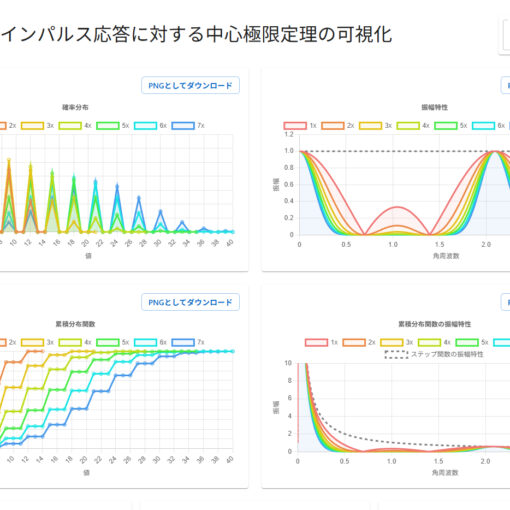
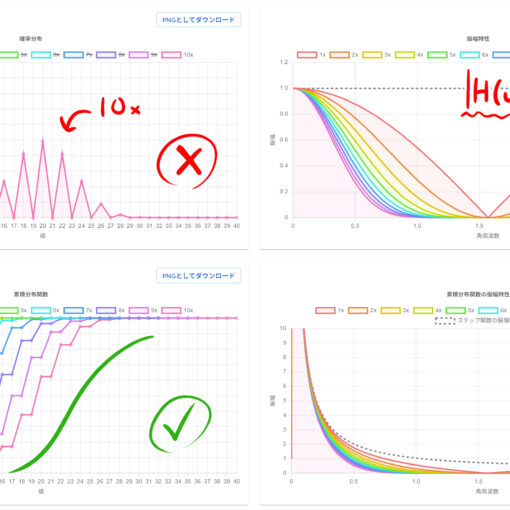
※ この記事は個人の感想であり、日記です。カルマンフィルタの説明を目的とするものではありませんが、誰かの理解の助けになるのであれば幸いです。
前提と結論
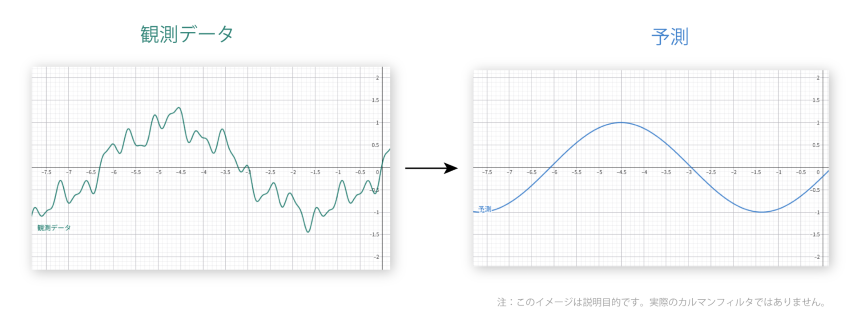
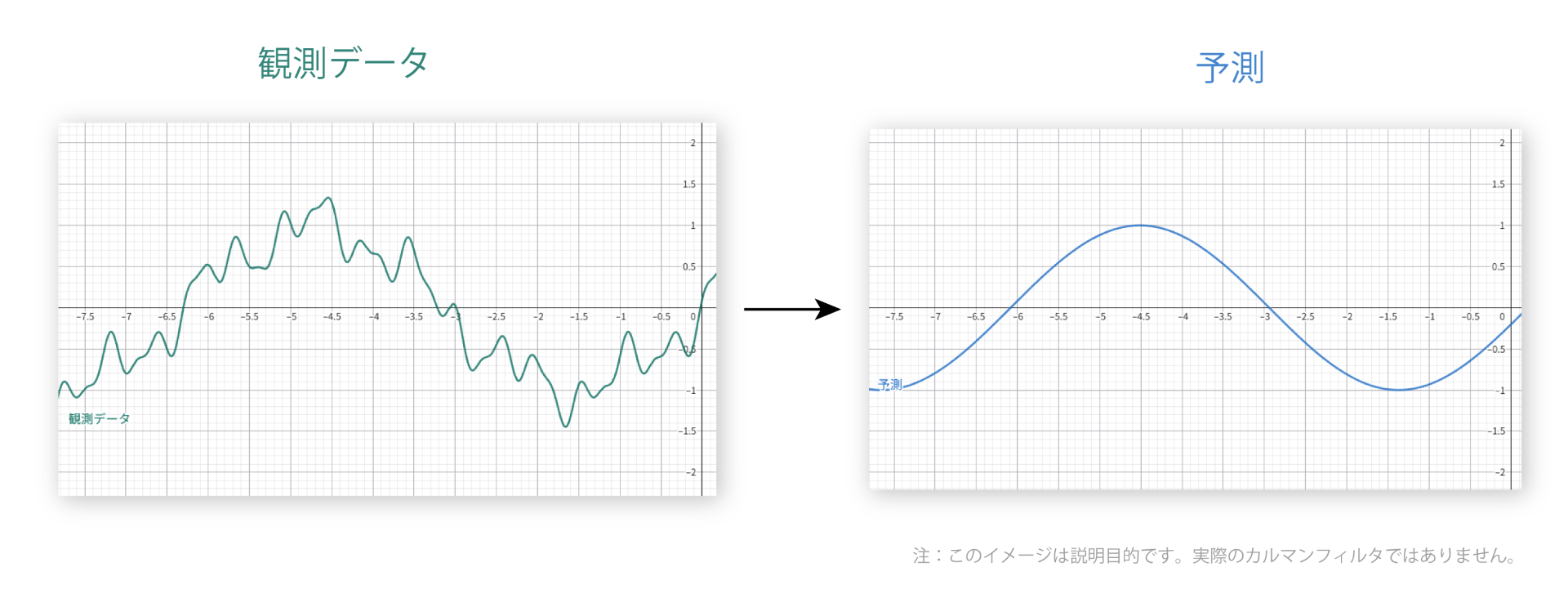
まず、カルマンフィルタとは、ノイズを含む観測データから真の物理量を推定するための数学的アルゴリズムである。
一方で、フィルタと言うと、個人的にはローパスフィルタやハイパスフィルタのような、線形時不変 (LTI) なエフェクトのことを想像してしまう。DTMer であればそれは自然な発想だろうと思う。
確かにその意味では、定常状態のカルマンフィルタはローパスフィルタに近い振る舞いを見せる。
しかし、カルマンフィルタはそのような意味での狭義の「フィルタ」にとどまらない。カルマンフィルタとは単なるローパスフィルタやバンドパスフィルタではなく、ベイズ推定を用いて、フィルタの係数を動的かつ逐次的に設計する統計的手法、およびそのようにして設計された「動的 (Time-Variant) フィルタ」のことなのである。
この記事を書くことになった経緯
Twitter をしていると、カルマンフィルタという言葉が目に入り、以下のような疑問が生じた。
- Wikipedia によれば、カルマンフィルタは IIR (無限インパルス応答)である
- IIR とは、過去の入力と出力に係数を掛けて足すだけの単純なシステムである
- 私は IIR および DSP (デジタル信号処理) に対する一定の理解を持っている
- にもかかわらず、なぜ Wikipedia のカルマンフィルタのページがこんなにも難しく、全く理解できないのか
- なぜ他のフィルタ(バターワースフィルタ等)のように、Wikipedia のカルマンフィルタのページに周波数特性が載っていないのか?
これに対する説明は最初に述べた通りである。
統計学には難しい数式がたくさん出てくるため、カルマンフィルタの説明にも難しい数式がたくさん出てくるのは当然である。(小学生レベルの結論)
また、多入力多出力であることも複雑さの理由になっていると考えられる。
具体例:定常状態のカルマンフィルタ(1 入力 1 出力)
具体例として、1 入力 1 出力のカルマンフィルタを考えてみる。単純化のため制御入力をゼロとする。
Wikipedia を見ると、カルマンフィルタの係数更新式が記載されているので、これを参考にする。十分な時間が経過した後の定常状態では、カルマンフィルタの係数は一定値に収束し、以下のような形になると考えられる。
$$
\hat{x}_{k|k} = F_k (I \;-\; K_k H_k) \hat{x}_{k-1|k-1} + K_k z_k
$$
特に、1 入力 1 出力の場合は、スカラー係数 a, b を用いて、以下のような形で書くことができる。
$$
\hat{x}_{k|k} = b z_k \;-\; a \hat{x}_{k-1|k-1}
$$
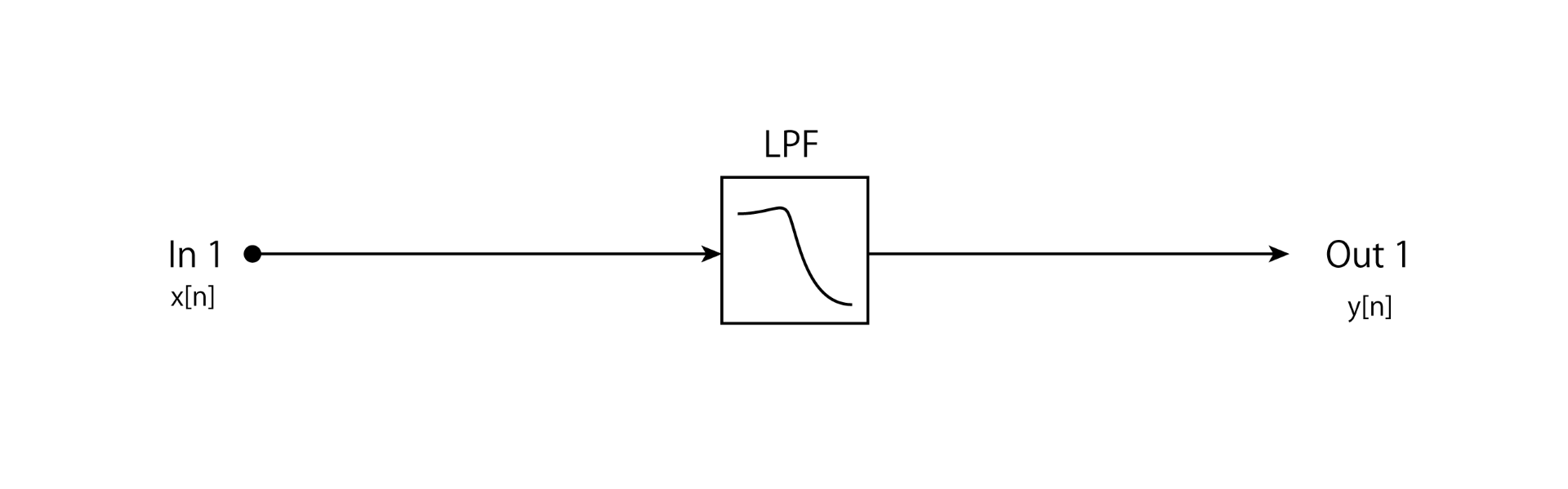
観測信号をシステムの入力 $x[n]$ 、推定値をシステムの出力 $y[n]$ と見なすと、これは 1 次の IIR 型ローパスフィルタであり、信号処理でよく用いられる以下のような形で表現することができる。
$$
y[n] = bx[n] \;-\; ay[n-1]
$$
カルマンフィルタの周波数特性(1 入力 1 出力の場合)
1 入力 1 出力のカルマンフィルタは、定常状態において、一次の IIR となることが分かった。
理解を深めるために、ここに一次 IIR のローパスフィルタの周波数特性の一例を掲載しておく。
$$
y[n] = Kx[n] + (1-K)y[n-1]
$$
$$
H(z) = \frac{Y(z)}{X(z)} = \frac{K}{1-(1-K)z^{-1}}
$$
$$
H(e^{j\omega}) = \frac{K}{1-(1-K)e^{-j\omega}}
$$
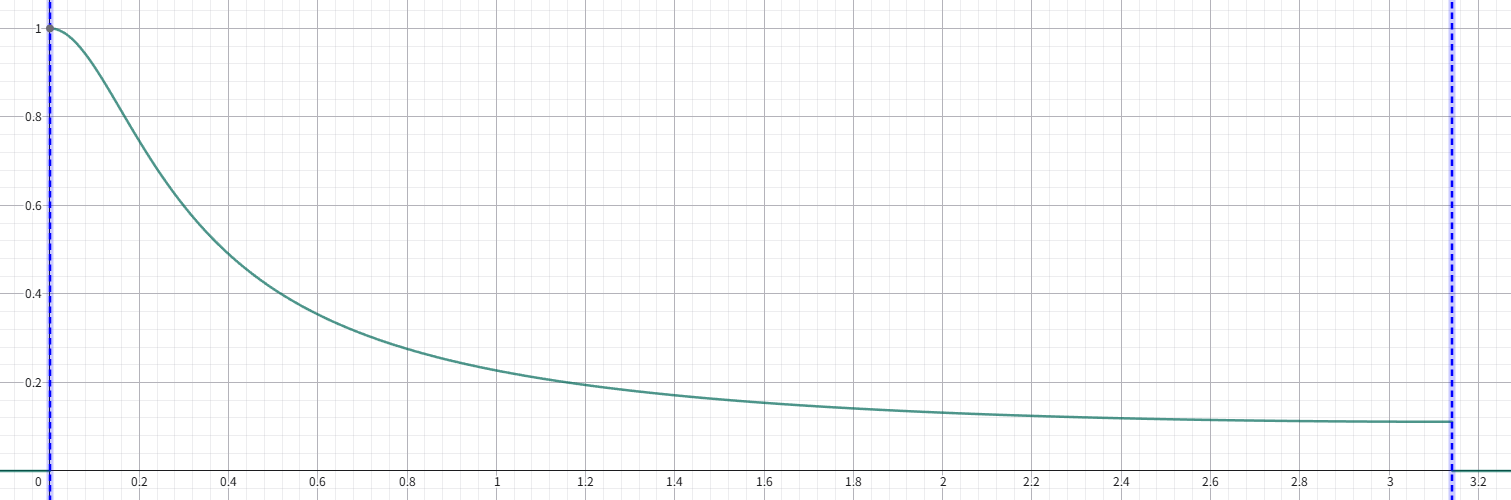
線形周波数・線形ゲイン(横軸:角周波数)
※ この周波数特性は一例です。
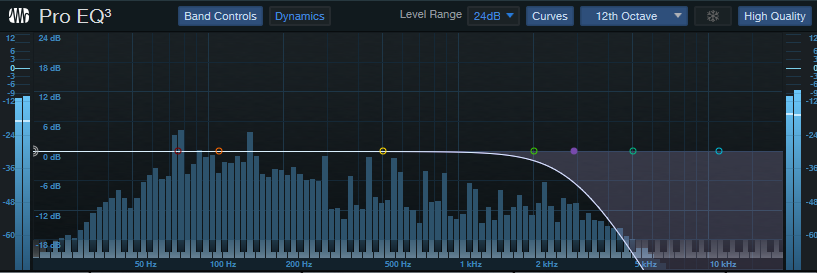
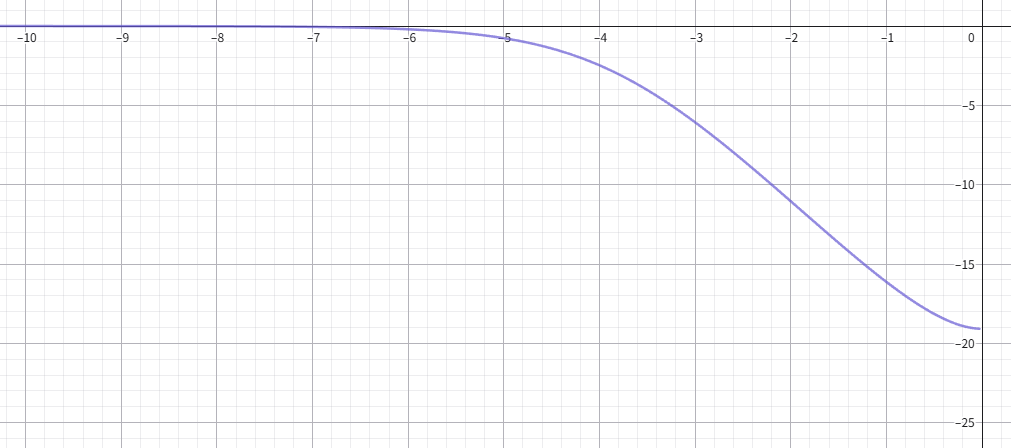
両対数(横軸:octave, 縦軸:dB)
※ この周波数特性は一例です。
特に面白みはない。
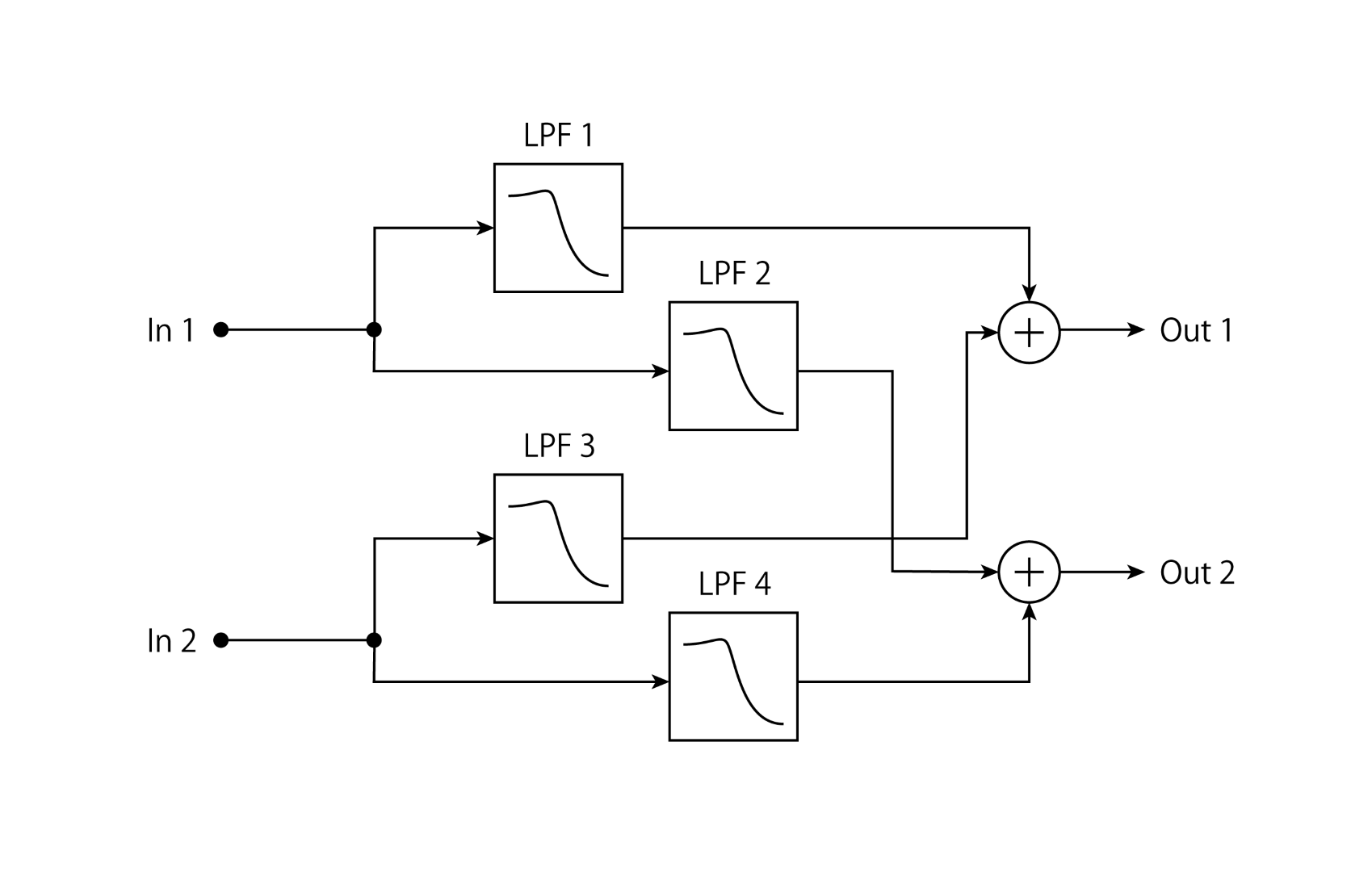
多入力・多出力の場合
多入力・多出力の場合でも、定常状態に限って考えれば、定常状態における線形性から、それぞれの入力と出力に対する IIR を考えればよい。n 入力 m 出力のカルマンフィルタでは、 $nm$ 個のインパルス応答が存在することになる。
※ ただし、それぞれのフィルタが必ずしも一次の IIR になるとは限らない。
カルマンフィルタが定常状態に至るまでの統計的アルゴリズム
最初に説明した通り、カルマンフィルタのアルゴリズムの本質とは、IIR フィルタそのものではなく、ベイズ確率にもとづいた統計的な推定プロセスである。
つまり、ここまでの説明によって、私がカルマンフィルタのアルゴリズムの本質について一切理解していないということがわかった。
いかがでしたか?
おまけ
Qiita にカルマンフィルタの周波数特性がバンドパス型になる例を画像で貼っている方がいらっしゃったので、参考リンクとして載せておきます。