中心極限定理の可視化（連載・インパルス応答と中心極限定理 2）

理論に踏み込む前に、実際に確率分布を計算することで、中心極限定理が成り立つことを視覚的に確認する。

六面サイコロ

確率変数として、六面サイコロの出目を考える。

$$
X \in \{1,2,3,4,5,6\}
$$

$$
\mathrm{P}(X = k) = \frac{1}{6} \quad (k = 1,2,3,4,5,6)
$$

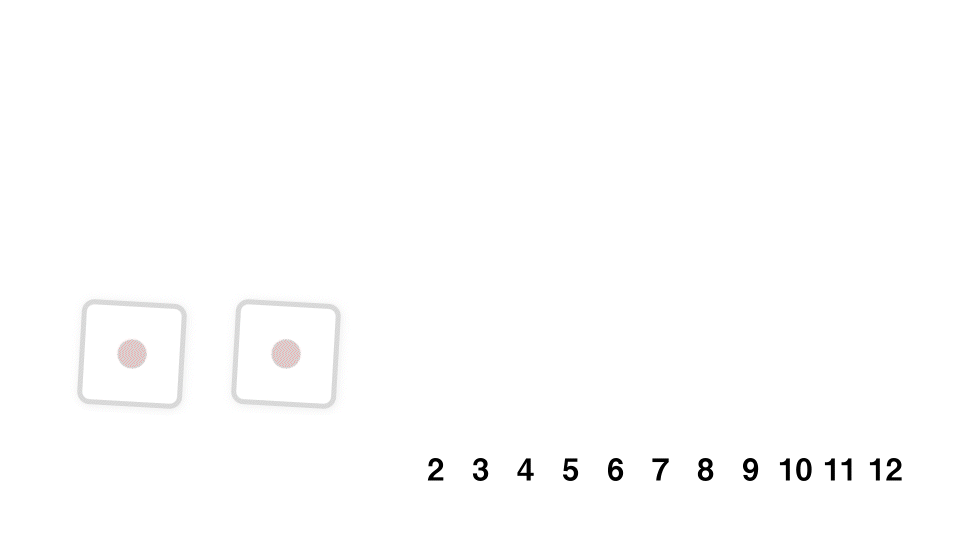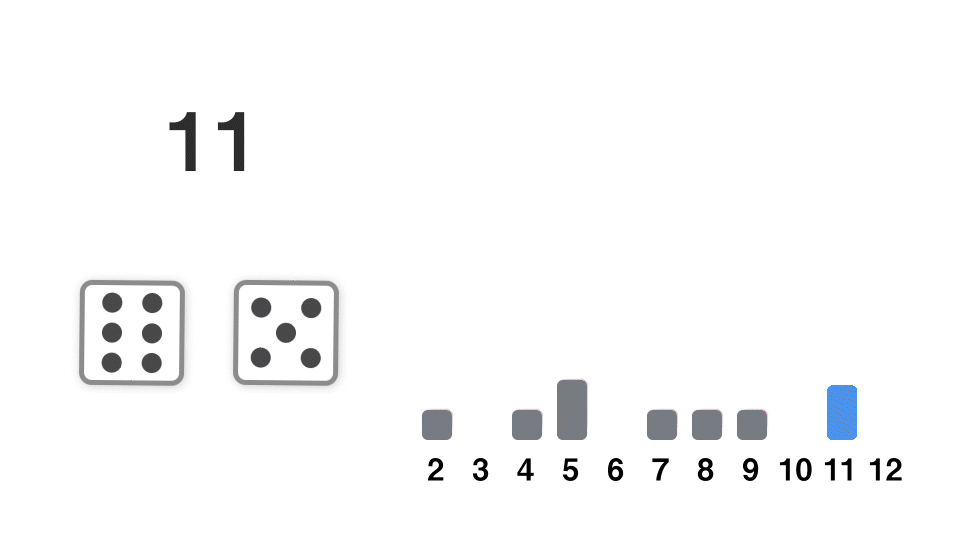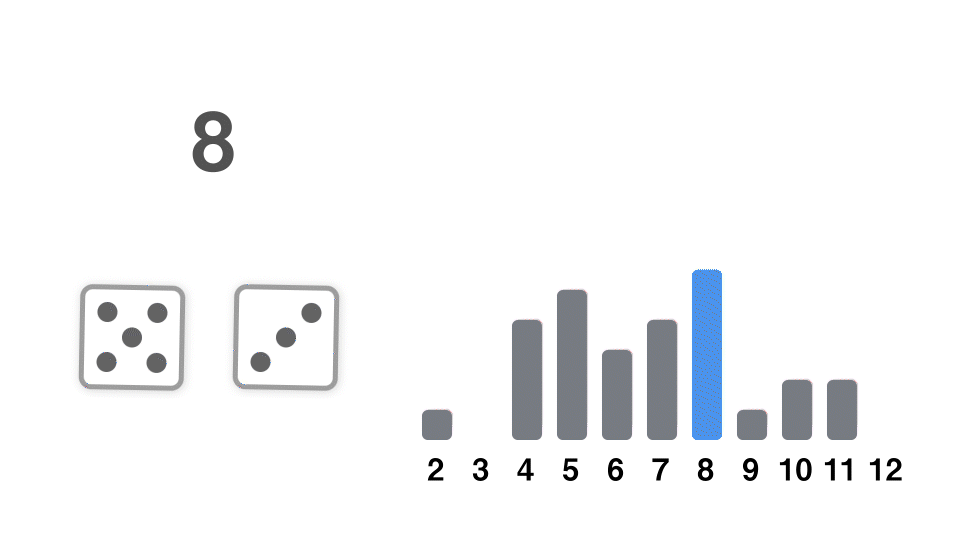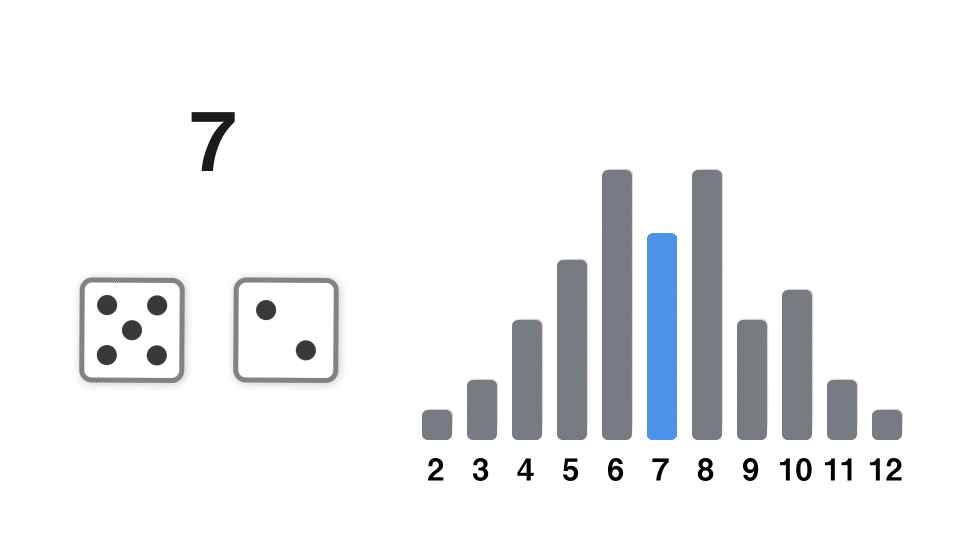
サイコロを振る独立な試行を何度も繰り返し、その出目の和を考える。例えば 2 回（2 個）の場合は、このようになる。

$$
S = X_1 + X_2
$$

36 通りに場合分けし、1 個目のサイコロの出目と、2 個目のサイコロの出目の和がちょうど k になる確率を考えることで、厳密な確率分布を計算することができる。便宜的に

$$
\mathrm{P}(X = k) = 0 \quad (k \ne 1,2,3,4,5,6)
$$

とすると、

$$
\mathrm{P}(S = k)
\,=\, \sum_{i=1}^{6}
\mathrm{P}(X_1 = i)\,
\mathrm{P}(X_2 = k \,-\, i)
$$

と書ける。

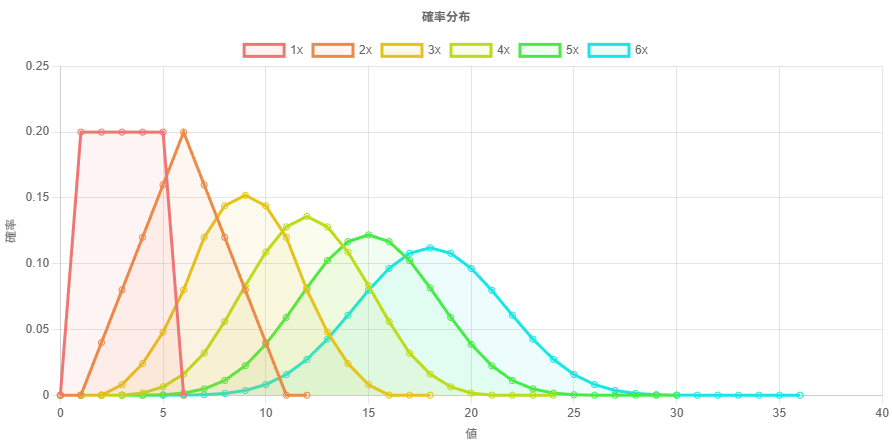
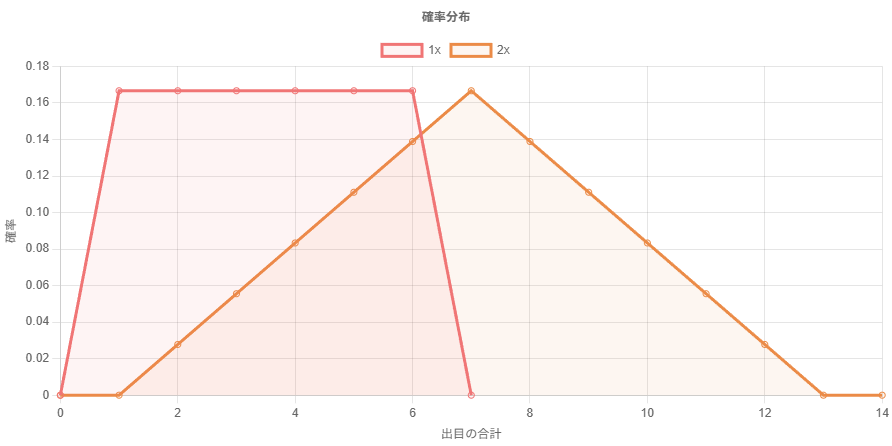
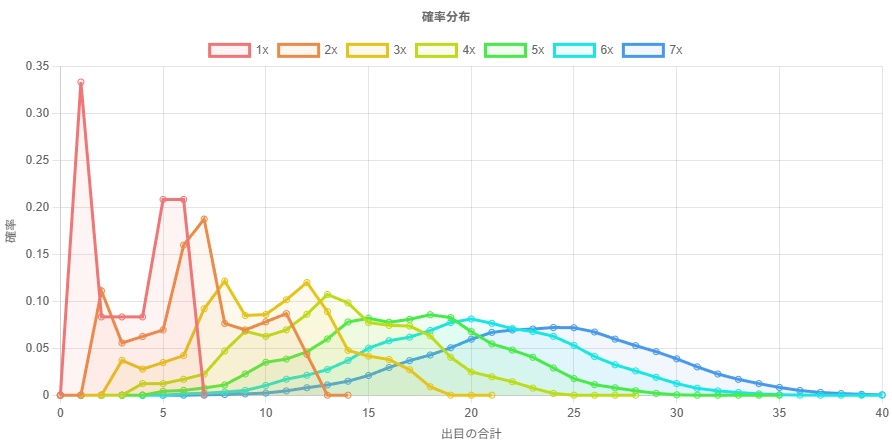
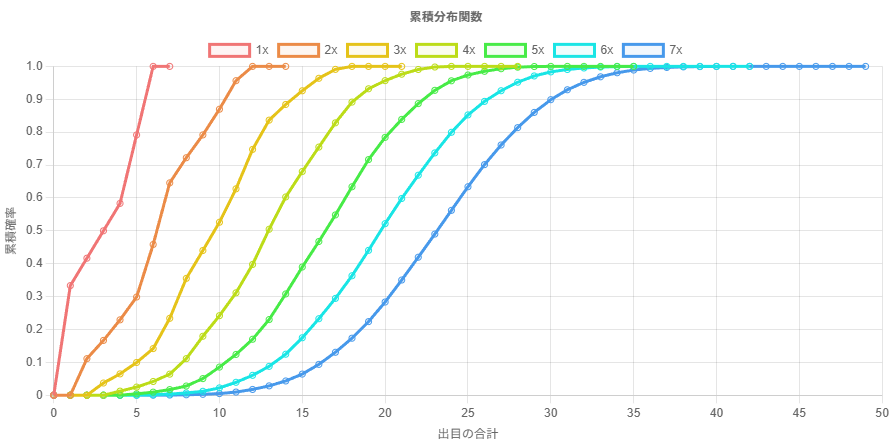
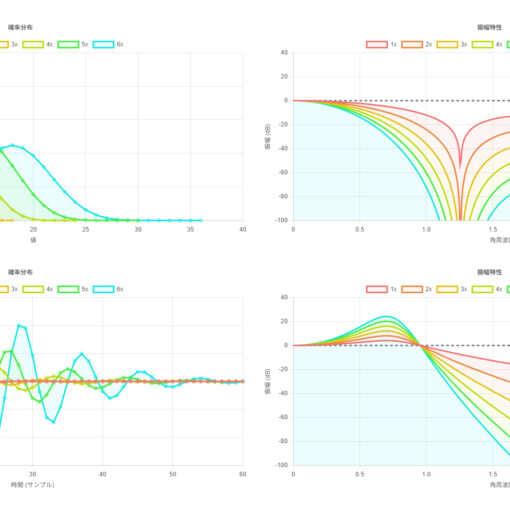
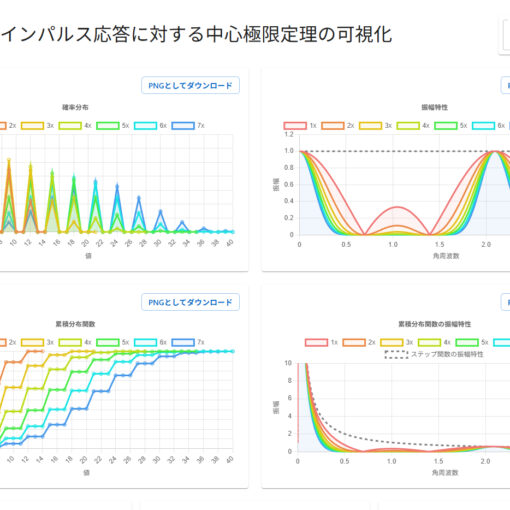
振るサイコロの数が増えていくとき、出目の合計の分布は正規分布に近付いていく。

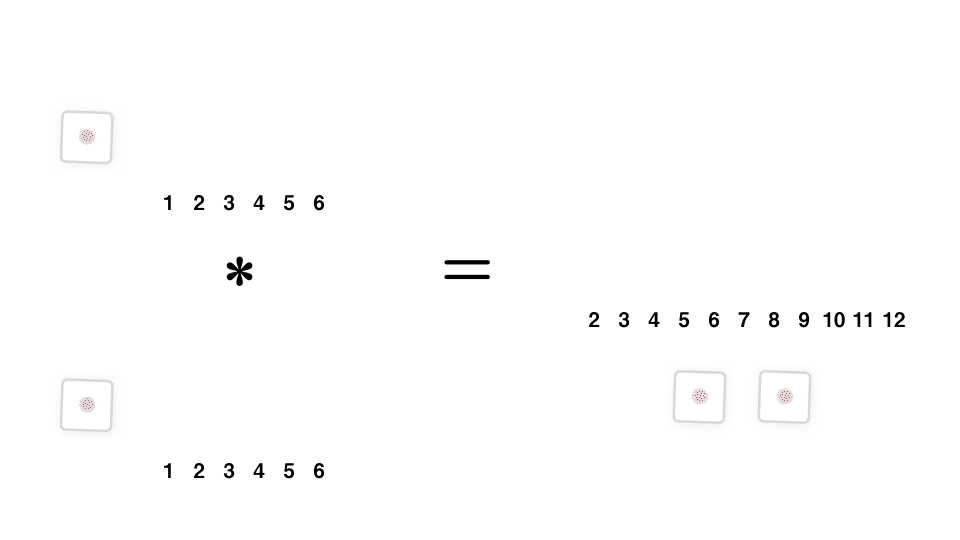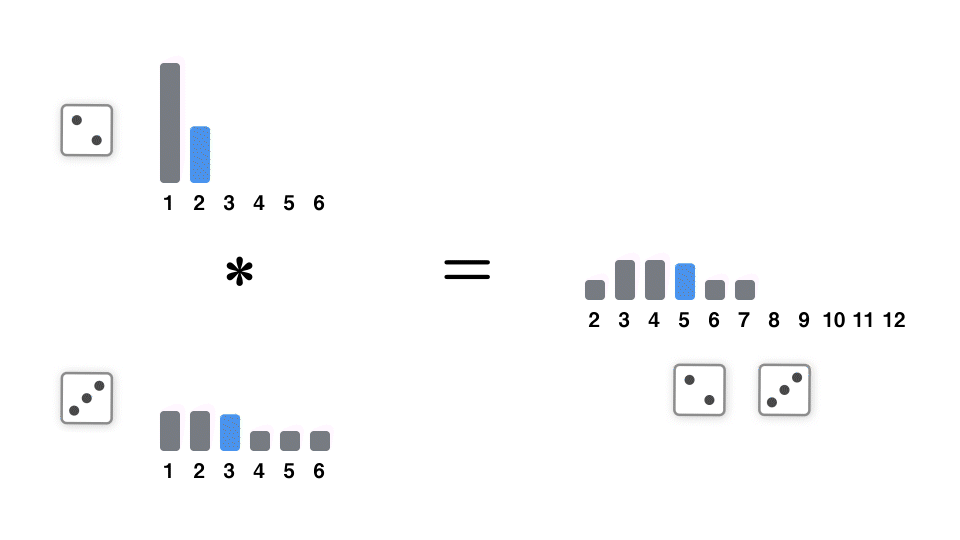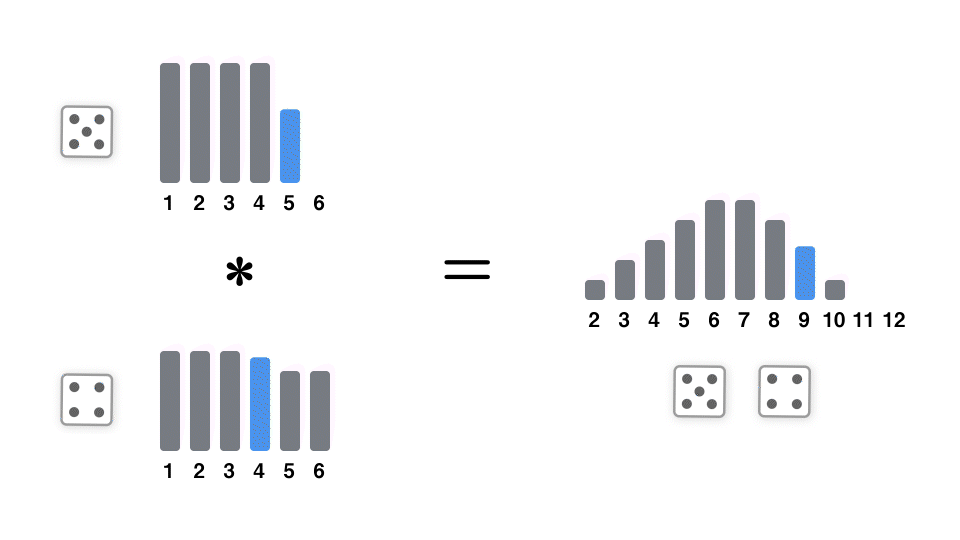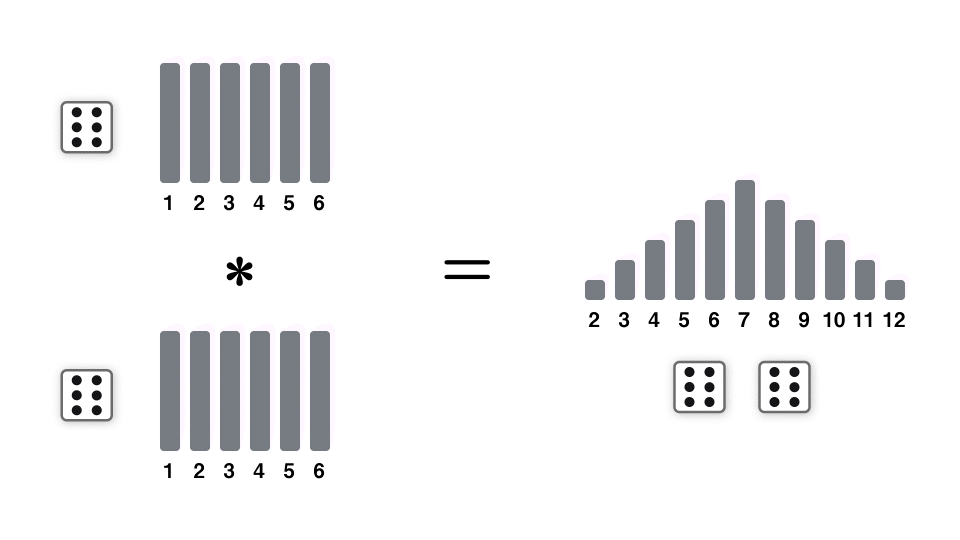
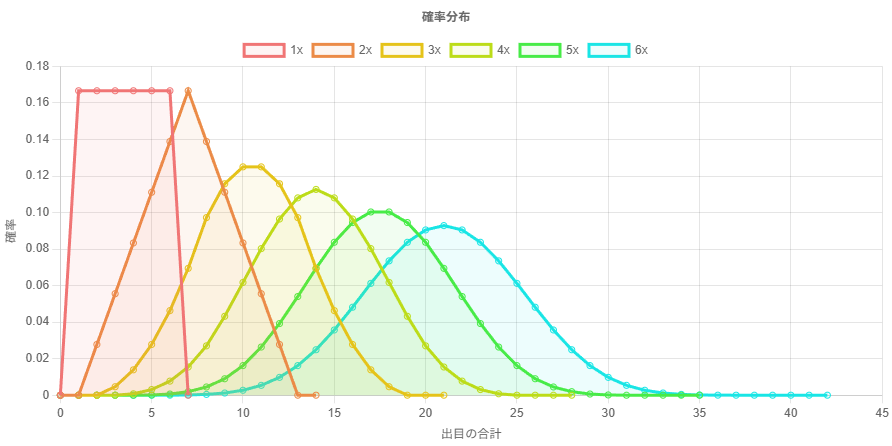
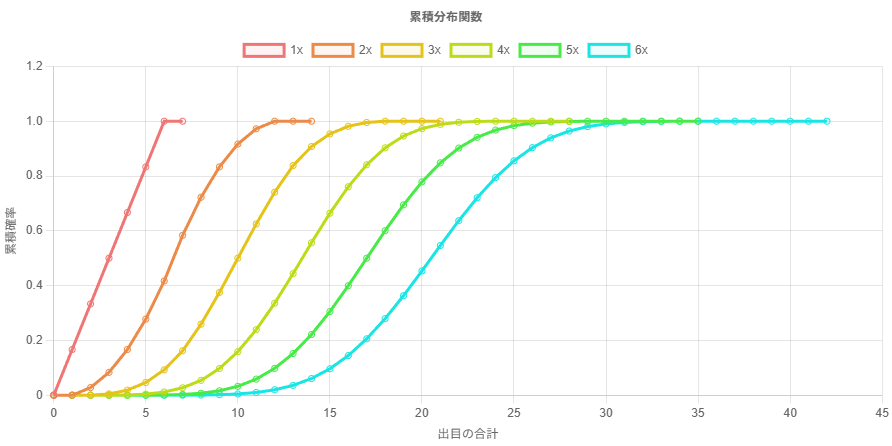
サイコロ 6 個までの出目の合計の確率分布をプロットしてみると、次第に正規分布に近付いていることがわかる。

この独立同分布な確率変数の和の確率質量関数（または確率密度関数）は、元の確率質量関数同士の畳み込みで表される。つまり、サイコロ 1 個を投げた場合の確率質量関数を、自己畳み込みすることで、サイコロを n 個投げた場合の確率質量関数を求めることができる。

$$
\mathrm{P}(Z = k)
\,=\, \sum_{i=-\infty}^{\infty}
\mathrm{P}(X = i)\,
\mathrm{P}(Y = k \,-\, i)
$$

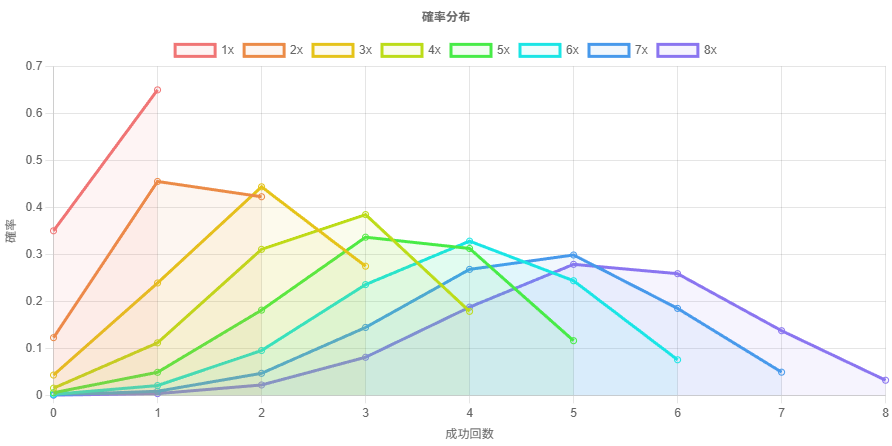
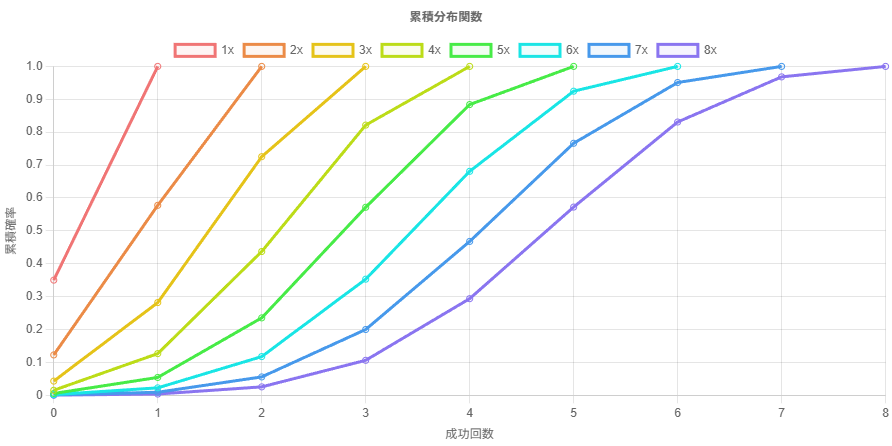
分布 X は左右対称である必要はない。例としてベルヌーイ分布で確認してみると、こちらも確かに正規分布に近付いていることがわかる。

$$
X \in \{0,1\}
$$

$$
\mathrm{P}(X = x) =
\begin{cases}
p & (x = 1) \\
1-p & (x = 0)
\end{cases}
$$

より奇妙な例として、各面の出る確率が等確率ではないような、いびつなサイコロを考える。

この場合でも、確かに正規分布に近付いていることがわかる。

関連した内容の動画を YouTube で見つけたので追記しておきます。