滑らかな max 関数「LogSumExp」と、タイムリマップでの加速【After Effects エクスプレッション】

フッテージを途中で 2 倍速にしたい場合、途中で動画の速度を変更すれば良いのですが、その場合、動きがリニアになってしまい、滑らかさが出ません。

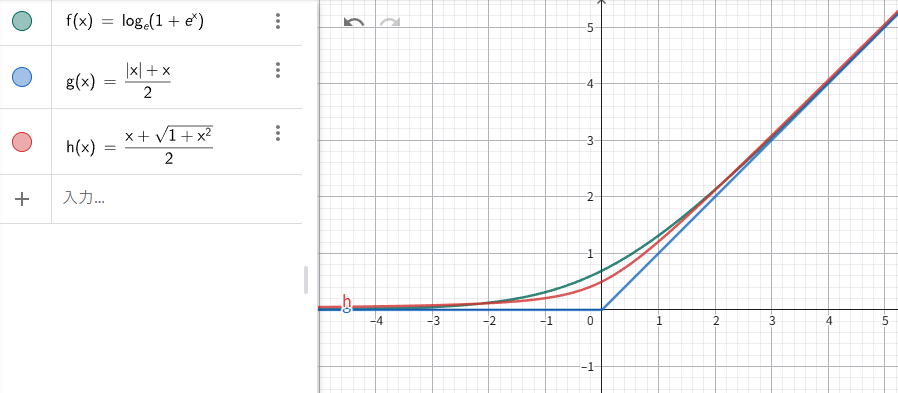
そこで、タイムリマップのエクスプレッションとして、max 関数

$$
\mathrm{max}(x_1,x_2,x_3,\cdots)
$$

を滑らかに近似した、 LogSumExp 関数

$$
\log_e(e^{x_1}+e^{x_2}+e^{x_3}+\cdots) \approx \mathrm{max}(x_1,x_2,x_3,\cdots)
$$

の一変数版の、「Softplus 関数」（SmoothReLU 関数）を使うことが出来ます。

$$
f(x)=\log_e(1+e^{x})\approx \mathrm{max}(0,x)
$$

正規化線形関数 – Wikipedia

Softplus – Wikipedia （英語版）

この関数を適切にシフトしたりスケーリングしたりして time に加えることで、任意の加速を実現することができます。

たとえば、このようなエクスプレッションになります。

time + 2 * Math.log(1 + Math.exp(time - 3))

詳しい計算

実際に詳しく計算してみます。

まず、Softplus を y 方向に a 倍して time に加えると、速度が 1 倍から (a+1) 倍に加速するようになります。

$$
\mathrm{TimeRemap}(t) = t + a\cdot f(t)
$$

次に、時間方向に $t_0$ シフトして、 $t_0$ 秒を中心として加速するようにします。

$$
\mathrm{TimeRemap}(t) = t + a\cdot\left\{f(t-t_0)-f(0-t_0)\right\}
$$

ここで、 $f(0-t_0)$ の補正は、 $t=0$ で $\mathrm{TimeRemap}(t)=0$ になるようにするための補正になります。

最後に、滑らかさを調整するため LogSumExp を縦横に 1/r 倍にスケーリングします。

$$
\mathrm{TimeRemap}(t) = t + a\cdot\left\{\frac{f(r(t-t_0))-f(r(0-t_0))}{r}\right\}
$$

完成したエクスプレッションは以下の通りです。

const t0 = 1;  // 速度変化の中心時刻
const r = 2.0;  // 速度変化の滑らかさ
const speedup = 1.0;  // 加速量

time + speedup * (
  Math.log(1 + Math.exp(r * (time - t0)))
  - Math.log(1 + Math.exp(r * (0 - t0)))
) / r

どちらが良いかは動画の用途にもよると思いますので、適切に判断してください。

補足：双曲線型の関数

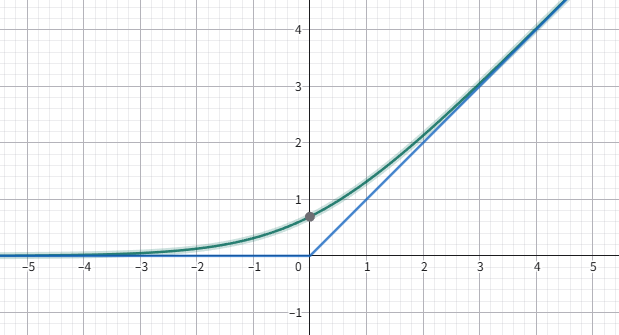
ただ、より扱いやすい双曲線型の関数

$$
h(x) = \frac{x + \sqrt{1 + x^2}}{2}
$$

で十分なのではないかと記事を書いてから気付きました。機会があったら記事を書き直します。

$$
\mathrm{TimeRemap}(t) = t + a\cdot\left\{h_r(t-t_0)-h_r(0-t_0)\right\}
$$

$$
h_r(x) = \frac{x + \sqrt{1/r^2 + x^2}}{2}
$$

a, r, $t_0$ の意味は先程と同じです。