中心極限定理の正しい意味（連載・インパルス応答と中心極限定理 5）

この記事では、工学的な実用性や一般的に推奨される理解を超えて（※自虐・自嘲）、「中心極限定理を適用できるための条件」と「中心極限定理における収束とは何か」について確認する。

(i) 中心極限定理を適用できるための 4 個の条件

中心極限定理を適用できるためにはいくつかの前提条件があった。

確率分布であること（大前提！！）
確率変数が独立であること
同分布であること
有限平均、有限分散であること

（※ここに、分散が 0 でないことを加える場合もあるが、この記事では加えないことにする。）

離散関数における解釈

この記事では、離散関数 $h[n]:\mathbb{Z}\to\mathbb{R}$ の自己畳み込みで、その関数がどのように変化するかを考えていた。

その場合、条件 1. は、確率質量関数に対しては非負かつ総和が 1 であることを言っている。

$$
h[n]\ge0
$$

$$
\sum_{n=-\infty}^{\infty} h[n]=1
$$

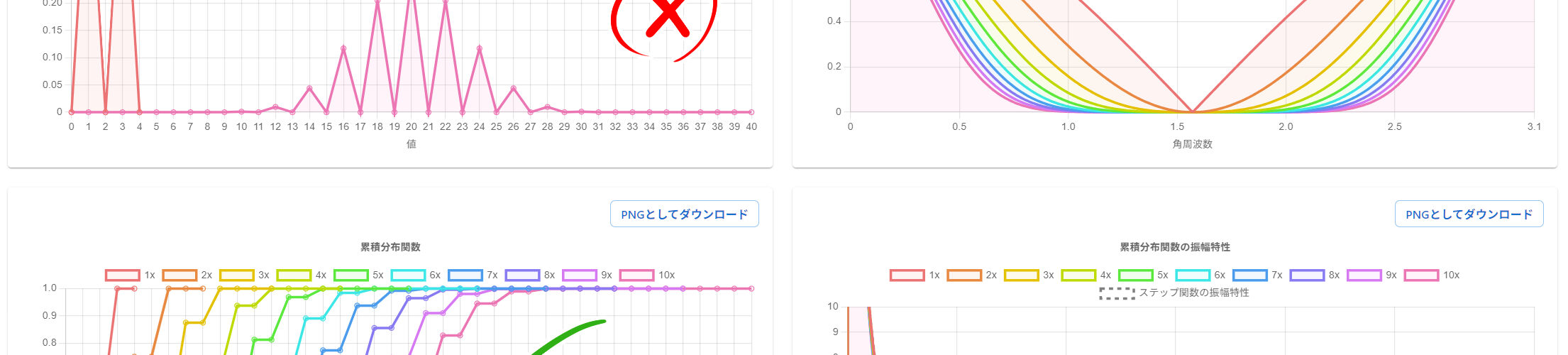
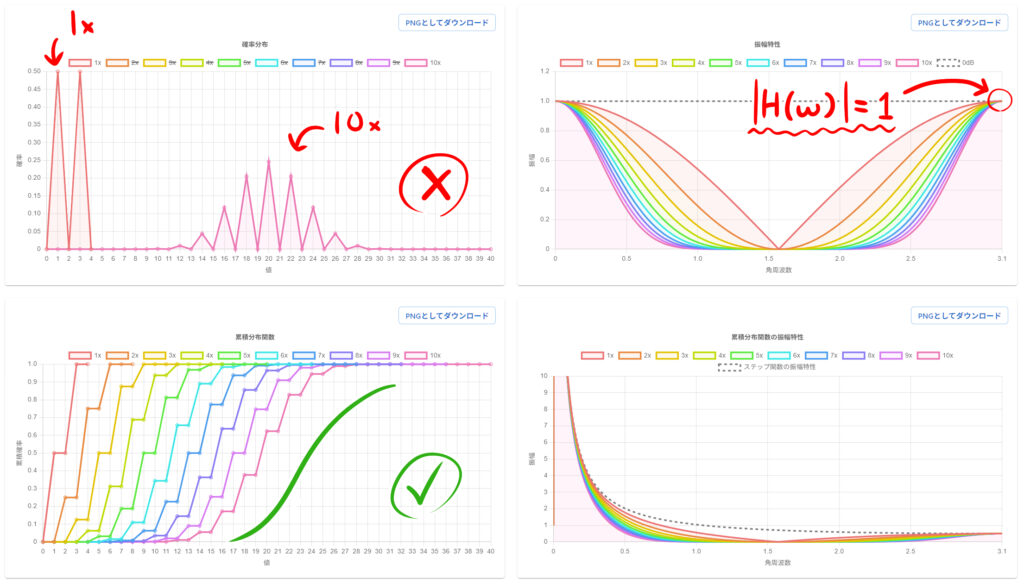
この段階で、前の記事で見た IIR ローパスフィルタの例は確率質量関数とは見做せなくなり、中心極限定理の適用対象から弾かれるのである！（※数学書でありがちな感嘆符）

なお、条件 1. を満たすとき、簡単な計算で、以下を示すことができる。（等号の有無に注意）

$$
\omega=0\implies H(\omega)=1
$$

$$
\omega\ne0\implies |H(\omega)|\le1
$$

条件 2. は合成確率を畳み込みで考えている時点で自動的に仮定している。

条件 3. も、この記事における前提としているため、満たしている。

条件 4. は限定的な条件であり、信号処理の分野で扱うことはほとんどないため、今回は省略する。分かりやすい例としては次ようなものがある。

$$
P(X = k) = \frac{1}{\zeta(3)} k^{-3} \quad (k \in \mathbb{Z}_+)
$$

$$
\zeta(3)=\sum_{n=1}^{\infty}n^{-3}
$$

(ii) そのとき、何が言えるか

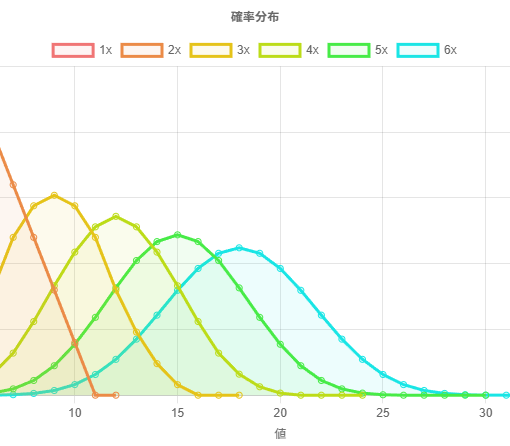
次に、中心極限定理が言えるときに、何が言えるのかを確認する。

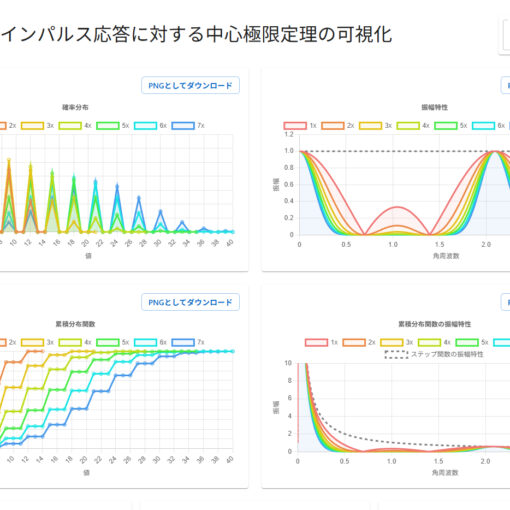
中心極限定理が成立するとき、適切にスケーリングすると、不連続な点を除いて、その累積分布関数が各点で正規分布の累積分布関数に収束する（＝分布収束）ことが言える。ここで、確率質量関数が収束することは言っていないことに注意する必要がある。

くし状ブラーの例

具体例として、次のようなフィルタを考えてみる。（仮にこれを「くし状ブラー」と呼ぶことにする。）

$$
y[n]=\frac12(x[n-2]+x[n+2])
$$

これは、次のような確率分布によく似ている。

$$
P(X = k) = \frac12 \qquad (k=\pm2)
$$

このフィルタでは、偶数番目と奇数番目のサンプルは決して混ざり合うことがないため、従って正規分布にも収束しない。しかし、この累積分布関数は、分散が大きくになるに従って段差が小さくなるため、正規分布の累積分布関数に収束するのである。

くし状ブラーの振幅特性

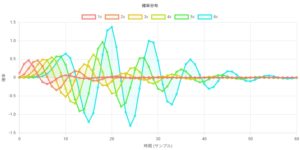
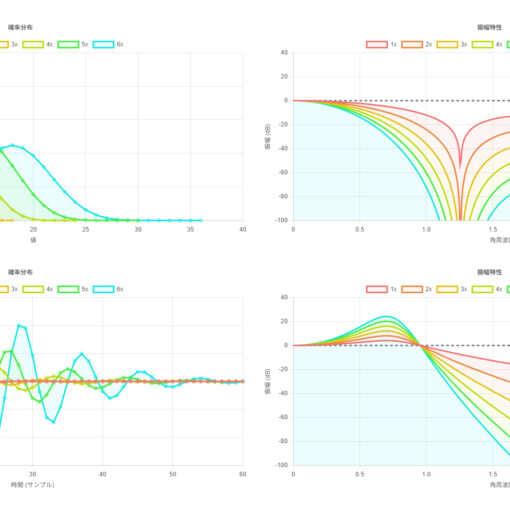
ここで、振幅特性（特性関数）のグラフに注目してみると、

$$
\omega\ne0\implies |H(\omega)|<1
$$

を満たしていないことがわかる。このとき、 $|H(\omega)|\ge1$ を何乗しても 0 には収束（一様収束）せず、決して高周波が弱まることがない。このように、確率質量関数が正規分布に収束しないということが、振幅特性によって判別できると考えられる。（ただし、細かい成立条件や逆については慎重に考える必要がある。）