一般の楕円の軸の傾き角と中心の座標を求める
一般の楕円について、傾き角と中心の座標を求める。まず、以下のような二次曲線を考える。
$$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$$
いま、これが楕円を表しているものとする。このとき、式変形によって、以下のように変形できるはずである。
$$
\frac{
\left\{ (x-x_0)\cos\theta+(y-y_0)\sin\theta \right\}^2
}{
a^2
}+\frac{
\left\{ -(x-x_0)\sin\theta+(y-y_0)\cos\theta \right\}^2
}{
b^2
}-1=0
$$
ただし、
$$a,b>0$$
$$-\frac{\pi}{4} \le \theta \le \frac{\pi}{4}$$
$$B^2-4AC<0$$
とする。
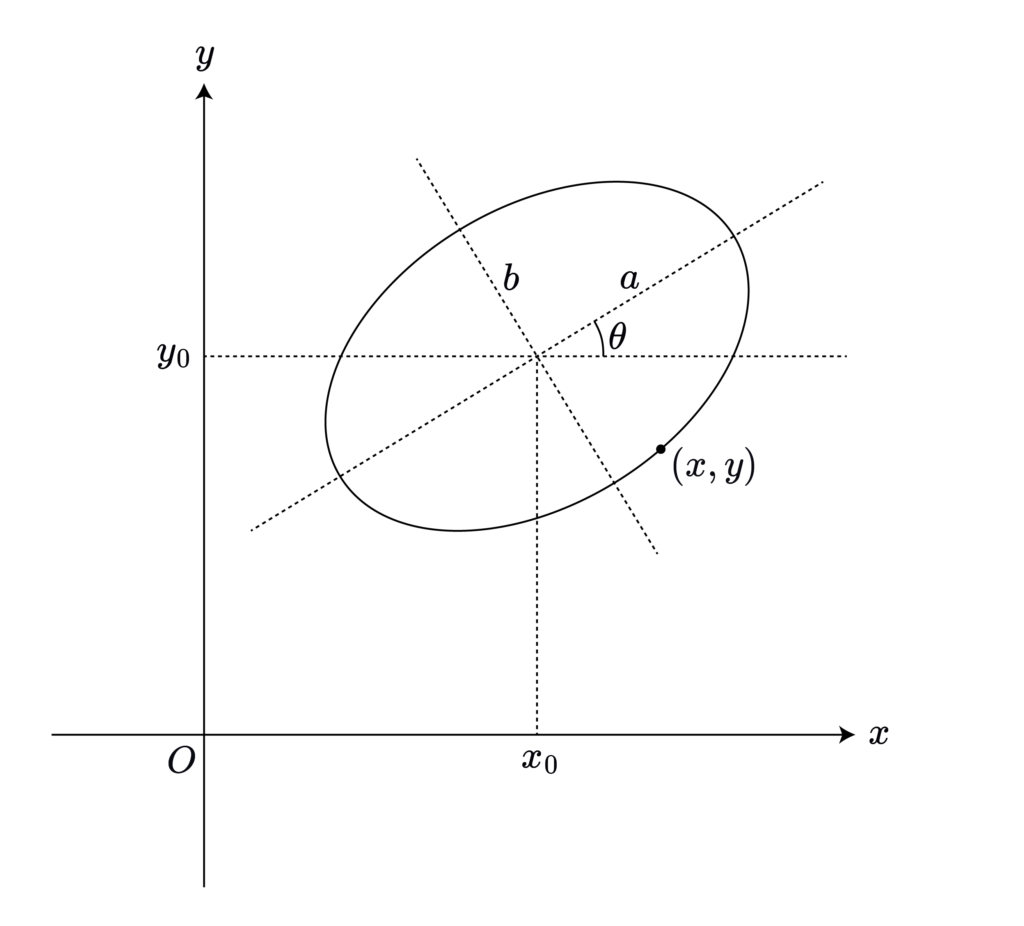
このとき、 $\theta,\: a,\: b,\: x_0,\: y_0$ を $A,\: B,\: C,\: D,\: E,\: F$ の式で表したい。
まず、2つの楕円の方程式を、 $(-x_0,-y_0)$ だけ平行移動させた後、 $-\theta$ だけ回転させる。
このとき、平行移動と回転変換を合成すると、
$$
\begin{cases}
X = (x-x_0)\cos\theta + (y-y_0)\sin\theta\\
Y = -(x-x_0)\sin\theta + (y-y_0)\cos\theta\\
\end{cases}
$$
のようになり、その逆変換は、
$$
\begin{cases}
x = X\cos\theta – Y\sin\theta + x_0\\
y = X\sin\theta + Y\cos\theta + y_0\\
\end{cases}
$$
となる。これを元の 2 つの楕円の方程式に代入すると、
$$
\frac{
X^2
}{
a^2
}+\frac{
Y^2
}{
b^2
}-1=0
$$
および、
$$
\begin{equation}
\begin{split}
&\: A(X\cos\theta – Y\sin\theta + x_0)^2 \\
\: + & \: B(X\cos\theta – Y\sin\theta + x_0)(X\sin\theta + Y\cos\theta + y_0)\\
\: + & \: C(X\sin\theta + Y\cos\theta + y_0)^2\\
\: + & \: D(X\cos\theta – Y\sin\theta + x_0)\\
\: + & \: E(X\sin\theta + Y\cos\theta + y_0)\\
\: + & \: F = 0\\
\end{split}
\end{equation}
$$
が得られる。2つ目の方程式を展開して整理すると、
$$
\begin{equation}
\begin{split}
&\: (A\cos^2\theta+B\cos\theta\sin\theta+C\sin^2\theta)X^2 \\
\: + & \: (-2A\cos\theta\sin\theta + B(\cos^2\theta-\sin^2\theta) + 2C\cos\theta\sin\theta)XY\\
\: + & \: (A\sin^2\theta-B\cos\theta\sin\theta+C\cos^2\theta)Y^2\\
\: + & \: \{ 2Ax_0\cos\theta + B(x_0\sin\theta+y_0\cos\theta) + 2Cy_0\sin\theta + D\cos\theta + E\sin\theta \}X\\
\: + & \: \{ -2Ax_0\sin\theta + B(x_0\cos\theta-y_0\sin\theta) + 2Cy_0\cos\theta – D\sin\theta + E\cos\theta \}Y\\
\: + & \: Ax_0^2+Bx_0y_0+Cy_0^2+Dx_0+Ey_0+F = 0\\
\end{split}
\end{equation}
$$
であり、非ゼロの定数倍が許容されていることに注意して係数を比較すると、 $\theta,\: a,\: b,\: x_0,\: y_0$ を求めることができる。まず $XY$ の係数から、
(i) $A=C,\:B=0$ のとき、$\theta$ は任意
(ii) $A=C,\:B\ne0$ のとき、
$$\theta=\pm\frac{\pi}{4}$$
(iii) $A \ne C$ のとき
$$\tan2\theta=\frac{B}{A-C}$$
が得られる。また $X$ 及び $Y$ の係数を見ると、 $x_0, y_0$ は連立一次方程式の形になるので、行列で表して逆行列を用いて解いた上で適当に因数分解すると、今は $4AC-B^2\ne0$ の条件を満たしているので、
$$
\begin{pmatrix}
x_0 \\
y_0 \\
\end{pmatrix}
=\frac{
1
}{
4AC-B^2
}\begin{pmatrix}
-2C & B \\
B & -2A \\
\end{pmatrix}\begin{pmatrix}
D \\
E \\
\end{pmatrix}
$$
と表せる。$a, b$ については $\theta,x_0,y_0$ を用いて、
$$
a^2 = -\frac{ Ax_0^2+Bx_0y_0+Cy_0^2+Dx_0+Ey_0+F }{ A\cos^2\theta+B\cos\theta\sin\theta+C\sin^2\theta }
$$
$$
b^2 = -\frac{ Ax_0^2+Bx_0y_0+Cy_0^2+Dx_0+Ey_0+F }{ A\sin^2\theta-B\cos\theta\sin\theta+C\cos^2\theta }
$$
と表せる。右辺が負になる場合は解がない。また、いずれかの分母が 0 になる場合も楕円にならないためここでは考えない。必要ならば半角の公式、$\sin$ の2倍角の公式、および三角関数の変換公式を使うこと。 $-\pi/4 \le \theta \le \pi/4$ であることを考慮すると、
(i) $-\pi/4 < \theta < \pi/4$ の場合、
$$
\cos^2\theta
= \frac{1+\cos2\theta}{2}
= \frac{1}{2} \left(1+\sqrt{\frac{1}{1+\tan^2 2\theta}}\right)
$$
$$
\sin^2\theta
= \frac{1-\cos2\theta}{2}
= \frac{1}{2} \left(1-\sqrt{\frac{1}{1+\tan^2 2\theta}}\right)
$$
$$
\cos\theta\sin\theta
= \frac{\sin2\theta}{2}
= \frac{\tan 2\theta}{2} \sqrt{\frac{1}{1+\tan^2 2\theta}}
$$
(ii) $\theta=\pm\pi/4$ の場合、 $\cos\theta=1/\sqrt{2},\:\:\sin\theta=\pm1/\sqrt{2}$
である。(複号同順)
感想
どうやって計算すれば良いか数時間悩んでいたが、そのまま係数比較するのではなく、図形を -θ 回転させてから係数比較することで、なんとか手計算可能な計算量まで落とし込めたのは良かった。
また、 $x_0,y_0$ を求める式から $\cos\theta,\:\sin\theta$ が綺麗に消えたときはびっくりした。
参考資料
資料1
補足の部分に $\tan2\theta$ を求める式が記載されている。B の係数に注意。
勉強しよう数学解答集: 原点の回りに回転した楕円の方程式から楕円の軸を計算する
https://schoolmathans.blogspot.com/2015/02/blog-post_14.html
資料2
二次曲線の回転角を求める計算が丁寧に記載されている。1次以下の項が平行移動に起因していて、2次曲線の形状にとって本質的ではないというのはその通りだったかもしれない。また、楕円以外の二次曲線についても言及していて、2次曲線が楕円になる条件も記載されている。
また、 $B^2-4AC<0$ を満たす場合に必ずしも楕円となるというわけではない、ということも記載されている。
【高校数学C】2次曲線の回転移動、標準化、判別式 | 受験の月
https://examist.jp/mathematics/quadratic-curve/nijikyokusen-hyoujyunka/
資料3
複素数や行列を用いた計算など。原点を中心とする楕円に関して $A>0, C>0$ という条件を加えると逆も成立することを示している。
斜めの楕円の方程式(特に45度回転) | 高校数学の美しい物語
https://manabitimes.jp/math/1124
資料4
半角の公式、$\sin$ の2倍角の公式、および三角関数の変換公式について
三角関数の公式の一覧 – Wikipedia
https://ja.wikipedia.org/wiki/三角関数の公式の一覧
一般の楕円の軸の傾き角と中心の座標を求める
一般の楕円について、傾き角と中心の座標を求める。まず、以下のような二次曲線を考える。
$$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$$
いま、これが楕円を表しているものとする。このとき、式変形によって、以下のように変形できるはずである。
$$
\frac{
\left\{ (x-x_0)\cos\theta+(y-y_0)\sin\theta \right\}^2
}{
a^2
}+\frac{
\left\{ -(x-x_0)\sin\theta+(y-y_0)\cos\theta \right\}^2
}{
b^2
}-1=0
$$
ただし、
$$a,b>0$$
$$-\frac{\pi}{4} \le \theta \le \frac{\pi}{4}$$
$$B^2-4AC<0$$ とする。
このとき、 $\theta,\: a,\: b,\: x_0,\: y_0$ を $A,\: B,\: C,\: D,\: E,\: F$ の式で表したい。
まず、2つの楕円の方程式を、 $(-x_0,-y_0)$ だけ平行移動させた後、 $-\theta$ だけ回転させる。
このとき、平行移動と回転変換を合成すると、
$$
\begin{cases}
X = (x-x_0)\cos\theta + (y-y_0)\sin\theta\\
Y = -(x-x_0)\sin\theta + (y-y_0)\cos\theta\\
\end{cases}
$$
のようになり、その逆変換は、
$$
\begin{cases}
x = X\cos\theta – Y\sin\theta + x_0\\
y = X\sin\theta + Y\cos\theta + y_0\\
\end{cases}
$$
となる。これを元の 2 つの楕円の方程式に代入すると、
$$
\frac{
X^2
}{
a^2
}+\frac{
Y^2
}{
b^2
}-1=0
$$
および、
$$
\begin{equation}
\begin{split}
&\: A(X\cos\theta – Y\sin\theta + x_0)^2 \\
\: + & \: B(X\cos\theta – Y\sin\theta + x_0)(X\sin\theta + Y\cos\theta + y_0)\\
\: + & \: C(X\sin\theta + Y\cos\theta + y_0)^2\\
\: + & \: D(X\cos\theta – Y\sin\theta + x_0)\\
\: + & \: E(X\sin\theta + Y\cos\theta + y_0)\\
\: + & \: F = 0\\
\end{split}
\end{equation}
$$
が得られる。2つ目の方程式を展開して整理すると、
$$
\begin{equation}
\begin{split}
&\: (A\cos^2\theta+B\cos\theta\sin\theta+C\sin^2\theta)X^2 \\
\: + & \: (-2A\cos\theta\sin\theta + B(\cos^2\theta-\sin^2\theta) + 2C\cos\theta\sin\theta)XY\\
\: + & \: (A\sin^2\theta-B\cos\theta\sin\theta+C\cos^2\theta)Y^2\\
\: + & \: \{ 2Ax_0\cos\theta + B(x_0\sin\theta+y_0\cos\theta) + 2Cy_0\sin\theta + D\cos\theta + E\sin\theta \}X\\
\: + & \: \{ -2Ax_0\sin\theta + B(x_0\cos\theta-y_0\sin\theta) + 2Cy_0\cos\theta – D\sin\theta + E\cos\theta \}Y\\
\: + & \: Ax_0^2+Bx_0y_0+Cy_0^2+Dx_0+Ey_0+F = 0\\
\end{split}
\end{equation}
$$
であり、非ゼロの定数倍が許容されていることに注意して係数を比較すると、 $\theta,\: a,\: b,\: x_0,\: y_0$ を求めることができる。まず $XY$ の係数から、
(i) $A=C,\:B=0$ のとき、$\theta$ は任意
(ii) $A=C,\:B\ne0$ のとき、
$$\theta=\pm\frac{\pi}{4}$$
(iii) $A \ne C$ のとき
$$\tan2\theta=\frac{B}{A-C}$$
が得られる。また $X$ 及び $Y$ の係数を見ると、 $x_0, y_0$ は連立一次方程式の形になるので、行列で表して逆行列を用いて解いた上で適当に因数分解すると、今は $4AC-B^2\ne0$ の条件を満たしているので、
$$
\begin{pmatrix}
x_0 \\
y_0 \\
\end{pmatrix}
=\frac{
1
}{
4AC-B^2
}\begin{pmatrix}
-2C & B \\
B & -2A \\
\end{pmatrix}\begin{pmatrix}
D \\
E \\
\end{pmatrix}
$$
と表せる。$a, b$ については $\theta,x_0,y_0$ を用いて、
$$
a^2 = -\frac{ Ax_0^2+Bx_0y_0+Cy_0^2+Dx_0+Ey_0+F }{ A\cos^2\theta+B\cos\theta\sin\theta+C\sin^2\theta }
$$
$$
b^2 = -\frac{ Ax_0^2+Bx_0y_0+Cy_0^2+Dx_0+Ey_0+F }{ A\sin^2\theta-B\cos\theta\sin\theta+C\cos^2\theta }
$$
と表せる。右辺が負になる場合は解がない。また、いずれかの分母が 0 になる場合も楕円にならないためここでは考えない。必要ならば半角の公式、$\sin$ の2倍角の公式、および三角関数の変換公式を使うこと。 $-\pi/4 \le \theta \le \pi/4$ であることを考慮すると、
(i) $-\pi/4 < \theta < \pi/4$ の場合、 $$ \cos^2\theta = \frac{1+\cos2\theta}{2} = \frac{1}{2} \left(1+\sqrt{\frac{1}{1+\tan^2 2\theta}}\right) $$ $$ \sin^2\theta = \frac{1-\cos2\theta}{2} = \frac{1}{2} \left(1-\sqrt{\frac{1}{1+\tan^2 2\theta}}\right) $$ $$ \cos\theta\sin\theta = \frac{\sin2\theta}{2} = \frac{\tan 2\theta}{2} \sqrt{\frac{1}{1+\tan^2 2\theta}} $$ (ii) $\theta=\pm\pi/4$ の場合、 $\cos\theta=1/\sqrt{2},\:\:\sin\theta=\pm1/\sqrt{2}$ である。(複号同順)
感想
どうやって計算すれば良いか数時間悩んでいたが、そのまま係数比較するのではなく、図形を -θ 回転させてから係数比較することで、なんとか手計算可能な計算量まで落とし込めたのは良かった。
また、 $x_0,y_0$ を求める式から $\cos\theta,\:\sin\theta$ が綺麗に消えたときはびっくりした。
参考資料
資料1
補足の部分に $\tan2\theta$ を求める式が記載されている。B の係数に注意。
資料2
二次曲線の回転角を求める計算が丁寧に記載されている。1次以下の項が平行移動に起因していて、2次曲線の形状にとって本質的ではないというのはその通りだったかもしれない。また、楕円以外の二次曲線についても言及していて、2次曲線が楕円になる条件も記載されている。
また、 $B^2-4AC<0$ を満たす場合に必ずしも楕円となるというわけではない、ということも記載されている。
資料3
複素数や行列を用いた計算など。原点を中心とする楕円に関して $A>0, C>0$ という条件を加えると逆も成立することを示している。
資料4
半角の公式、$\sin$ の2倍角の公式、および三角関数の変換公式について