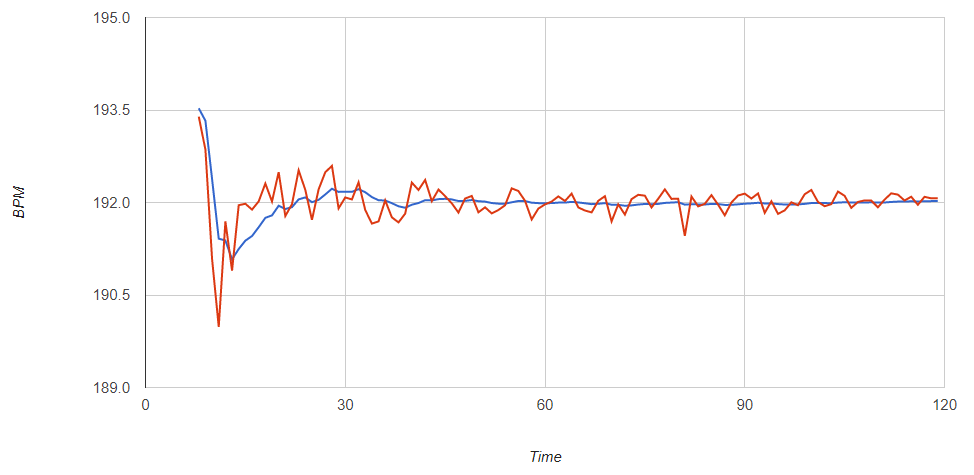
これは Math Advent Calendar 2017 6日目の記事です。
はじめに
ベイズBPM計測器は、曲に合わせて手動でスペースキーを押すとBPMを測定してくれるツールです。
今日は、スペースキーが押された時刻から、ベイズの定理を用いてBPMを推定する方法について考えたいと思います。
観測データ
まず、スペースキーが入力された時刻を
\[ T_n \quad (0 \leq n \leq N) \]
（ミリ秒）とし、スペースキーが入力された時刻の間隔を
\[ a_n = T_{n+1} – T_n \quad (0 \leq n \leq N – 1)\]
と定義します。
簡単な推定方法
BPMの簡単な推定方法として、最後にキーが押された時刻と最初にキーが押された時刻の差を取って、(キーが押された回数 – 1) で割る、という方法があります。
\[ E = \frac{1}{N} \times ( T_N – T_0 ) = \frac{1}{N} \times \sum_{i=0}^{N-1} a_i \]
しかしこの方法では、最初のキー入力と最後のキー入力以外の時刻が計算結果に影響していません。これは得られた情報を最大限に利用してBPM推定するアルゴリズムとは考えづらいと予想できます。本当でしょうか？ では考えてみましょう。
事前分布
楽曲の本来のBPMから計算される1拍の長さを $$ 2u $$ 、最初の拍と最後の拍が鳴る時刻の（相加）平均を $$ t $$ とすると、$$ i $$ 拍目の時刻は
\[ t + (-N + 2i)u \quad (0 \leq i \leq N) \]
となります。ここで、t と u が事前分布として一様分布を取る場合を考えます。つまり、BPM 180の曲が与えられる確率と、BPM 150の曲が与えられる確率と、BPM 120の曲が与えられる確率がどれも等しいということを意味します。これは、ある程度妥当な仮定だと考えられます。
スペースキーを人間が押す時刻が、この時刻を中心とする独立で分散が $$ \sigma^2 $$ の正規分布に従うと仮定すると、時刻 $$ x $$ に $$ i $$ 回目のキーが入力される確率は次のように表されます。
\[ p_i(x) = \mathcal{N}(t – Nu + 2iu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{\{x – (t – Nu + 2iu)\}^2}{2 \sigma^2} \right) \]
N=3 の場合
話を簡単にするために、N = 3 と固定して考えてみましょう。この場合、0、1、2、3拍目の時刻はそれぞれ
\[ t – 3u, \quad t – u, \quad t + u, \quad t + 3u \]
となります。従って、時刻 $$ x $$ に0、1、2、3回目のキーが入力される確率はそれぞれ次のように表されます。
\[ \begin{split} p_0(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{\{x – (t – 3u)\}^2}{2 \sigma^2} \right) \\ p_1(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{\{x – (t – u)\}^2}{2 \sigma^2} \right) \\ p_2(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{\{x – (t + u)\}^2}{2 \sigma^2} \right) \\ p_3(x) &= \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{\{x – (t + 3u)\}^2}{2 \sigma^2} \right) \end{split} \]
また、実際に観測されたキー入力の時刻は、次のように表されます。
\[ T_0, \quad T_1, \quad T_2, \quad T_3 \]
ここで、一般性を失わずに $$ T_0 = 0 $$ とすると、スペースキーが入力された時刻の間隔 $$ a_i $$ を用いて次のように表すことができます。
\[ \begin{split} T_0 &= 0 \\ T_1 &= a_0 \\ T_2 &= a_0 + a_1 \\ T_3 &= a_0 + a_1 + a_2 \end{split} \]
ある t と u の値が与えられた場合にこの実現値が観測される確率密度関数は
\[ p(a_0, a_1, a_2 \, | \, t, u) = p_0(0) \cdot p_1(a_0) \cdot p_2(a_0 + a_1) \cdot p_3(a_0 + a_1 + a_2) \]
と表すことができます。
事後確率と1拍の長さの計算
t と u を、閉区間 [-L, L] で一様な値を取る分布とすると、このことは次のような式で表すことが出来ます。
\[ p(t, u) = \frac{1}{4L^2} \quad (-L \leq t, u \leq L) \]
また、この範囲の任意の t, u に対して $$ a_0, a_1, a_2 $$ が観測される確率は、次のように計算できます。
\[ p(a_0, a_1, a_2) = \int_{-L}^{L} \int_{-L}^{L} p(a_0, a_1, a_2 \, | \, t, u) \, p(t, u) \, \mathrm{d}t\mathrm{d}u \]
さて、ベイズの定理より、
\[ p(t, u \, | \, a_0, a_1, a_2) = \frac{p(a_0, a_1, a_2 \, | \, t, u) \, p(t, u)}{p(a_0, a_1, a_2)} \]
となりますので、上の式を代入して約分すると次のようになります
\[ p(t, u \, | \, a_0, a_1, a_2) = \frac{p_0(0) \cdot p_1(a_0) \cdot p_2(a_0 + a_1) \cdot p_3(a_0 + a_1 + a_2)}{\int_{-L}^{L} \int_{-L}^{L} p_0(0) \cdot p_1(a_0) \cdot p_2(a_0 + a_1) \cdot p_3(a_0 + a_1 + a_2) \, \mathrm{d}t\mathrm{d}u} \]
ところで、この確率密度関数は $$ a_0, a_1, a_2 $$ が観測された場合の t, u の確率密度関数ですから、u に関して期待値を取れば、1拍の長さの推定値が得られることになります。u の期待値を計算すると、次のようになります。
\[ E = \int_{-L}^{L} \int_{-L}^{L} p(t, u \, | \, a_0, a_1, a_2) \cdot u \, \mathrm{d}t\mathrm{d}u \]
実際に計算してみた
では、まずは分母の $$ p(a_0, a_1, a_2) $$ から計算していきましょう。被積分関数は $$ p(a_0, a_1, a_2 \, | \, t, u) $$ と $$ p(t, u) $$ の積ですが、前者は
\[ \begin{split} p(a_0, a_1, a_2 \, | \, t, u) &= p_0(0) \cdot p_1(a_0) \cdot p_2(a_0 + a_1) \cdot p_3(a_0 + a_1 + a_2) \\ &= \frac{1}{(2\pi\sigma^2)^2} \exp\left( -\frac{\{0 – (t – 3u)\}^2}{2 \sigma^2} \right) \exp\left( -\frac{\{a_0 – (t – u)\}^2}{2 \sigma^2} \right) \\ & \quad\quad\quad\quad \times \exp\left( -\frac{\{a_0 + a_1 – (t + u)\}^2}{2 \sigma^2} \right) \exp\left( -\frac{\{a_0 + a_1 + a_2 – (t + 3u)\}^2}{2 \sigma^2} \right) \\ &= \frac{1}{(2\pi\sigma^2)^2} \exp\left( -\frac{\{0 – (t – 3u)\}^2 + \{a_0 – (t – u)\}^2 + \{a_0 + a_1 – (t + u)\}^2 + \{a_0 + a_1 + a_2 – (t + 3u)\}^2}{2 \sigma^2} \right) \\ &= \frac{1}{(2\pi\sigma^2)^2} \exp\left( -\frac{ 3a_0^2 + 2a_1^2 + a_2^2+ 2(a_0a_1 + a_1a_2 + a_2a_0) + 4t^2 – 2(3a_0 + 2a_1 + a_2)t + 20u^2 – 2(3a_0 + 4a_1 + 3a_2)u }{2 \sigma^2} \right) \end{split} \]
となるので、ゴリゴリと計算すると次のようになります。（一部で途中式を省略しています）
\[ \begin{split} & p(a_0, a_1, a_2) \\ &= \int_{-L}^{L} \int_{-L}^{L} p(a_0, a_1, a_2 \, | \, t, u) \, p(t, u) \, \mathrm{d}t\mathrm{d}u \\ &= \frac{1}{4L^2} \int_{-L}^{L} \int_{-L}^{L} p(a_0, a_1, a_2 \, | \, t, u) \, \mathrm{d}t\mathrm{d}u \\ &= \frac{1}{4L^2 (2\pi\sigma^2)^2} \int_{-L}^{L} \biggl\{ \exp\left(-\frac{ – \frac{(3a_0 + 2a_1 + a_2)^2}{4} + 3a_0^2 + 2a_1^2 + a_2^2+ 2(a_0a_1 + a_1a_2 + a_2a_0) + 20u^2 – 2(3a_0 + 4a_1 + 3a_2)u }{2 \sigma^2}\right) \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{4}{2 \sigma^2}\left(t – \frac{3a_0 + 2a_1 + a_2}{4}\right)^2 \right) \, \mathrm{d}t \biggr\} \mathrm{d}u \\ &= \frac{1}{4L^2 (2\pi\sigma^2)^2} \\ & \quad\quad \times \int_{-L}^{L} \exp\left(-\frac{ – (3a_0 + 2a_1 + a_2)^2 + 4\{\cdots + 20u^2 – 2(3a_0 + 4a_1 + 3a_2)u\} }{8 \sigma^2}\right)\mathrm{d}u \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{4}{2 \sigma^2}\left(t – \frac{3a_0 + 2a_1 + a_2}{4}\right)^2 \right) \, \mathrm{d}t \\ &= \frac{1}{4L^2 (2\pi\sigma^2)^2} \\ & \quad\quad \times \exp\left(-\frac{ – (3a_0 + 4a_1 + 3a_2)^2 – 5(3a_0 + 2a_1 + a_2)^2 + 20(3a_0^2 + 2a_1^2 + a_2^2) + 40(a_0a_1 + a_1a_2 + a_2a_0) }{40 \sigma^2}\right) \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{80}{8 \sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \, \mathrm{d}u \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{4}{2 \sigma^2}\left(t – \frac{3a_0 + 2a_1 + a_2}{4}\right)^2 \right) \, \mathrm{d}t \\ &= \frac{C}{4L^2 (2\pi\sigma^2)^2} \\\end{split} \]
ただしCは定数となります。ここではまだCは計算しません。
期待値の計算
次に $$ E $$ を計算します。上の計算とほぼ一緒なので簡単です。（一部で途中式を省略しています）
\[ \begin{split} E &= \int_{-L}^{L} \int_{-L}^{L} p(t, u \, | \, a_0, a_1, a_2) \cdot u \, \mathrm{d}t\mathrm{d}u \\ &= \int_{-L}^{L} \int_{-L}^{L} \frac{p(a_0, a_1, a_2 \, | \, t, u) \, p(t, u)}{p(a_0, a_1, a_2)} \cdot u \, \mathrm{d}t\mathrm{d}u \\ &= \frac{1}{4L^2} \cdot \frac{4L^2 (2\pi\sigma^2)^2}{C} \int_{-L}^{L} \int_{-L}^{L} p(a_0, a_1, a_2 \, | \, t, u) \cdot u \, \mathrm{d}t\mathrm{d}u \\ &= \frac{(2\pi\sigma^2)^2}{C} \int_{-L}^{L} \int_{-L}^{L} p(a_0, a_1, a_2 \, | \, t, u) \cdot u \, \mathrm{d}t\mathrm{d}u \\ &= \frac{1}{C} \int_{-L}^{L} \int_{-L}^{L} \exp\left( -\frac{ \cdots + 4t^2 – 2(3a_0 + 2a_1 + a_2)t + 20u^2 – 2(3a_0 + 4a_1 + 3a_2)u }{2 \sigma^2} \right) \cdot u \, \mathrm{d}t\mathrm{d}u \\ &= \frac{1}{C} \int_{-L}^{L} \biggl\{ \exp\left(-\frac{ – \frac{(3a_0 + 2a_1 + a_2)^2}{4} + \cdots + 20u^2 – 2(3a_0 + 4a_1 + 3a_2)u }{2 \sigma^2}\right) \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{4}{2 \sigma^2}\left(t – \frac{3a_0 + 2a_1 + a_2}{4}\right)^2 \right) \, \mathrm{d}t \biggr\} \cdot u \, \mathrm{d}u \\ &= \frac{1}{C} \int_{-L}^{L} \exp\left(-\frac{ – (3a_0 + 2a_1 + a_2)^2 + 4\{\cdots + 20u^2 – 2(3a_0 + 4a_1 + 3a_2)u\} }{8 \sigma^2}\right) \cdot u \, \mathrm{d}u \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{4}{2 \sigma^2}\left(t – \frac{3a_0 + 2a_1 + a_2}{4}\right)^2 \right) \, \mathrm{d}t \\ &= \frac{1}{C} \times \exp\left(-\frac{ – (3a_0 + 4a_1 + 3a_2)^2 – 5(3a_0 + 2a_1 + a_2)^2 + 20(3a_0^2 + 2a_1^2 + a_2^2) + 40(a_0a_1 + a_1a_2 + a_2a_0) }{40 \sigma^2}\right) \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{80}{8 \sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \cdot u \, \mathrm{d}u \\ & \quad\quad \times \int_{-L}^{L} \exp\left( -\frac{4}{2 \sigma^2}\left(t – \frac{3a_0 + 2a_1 + a_2}{4}\right)^2 \right) \, \mathrm{d}t \\ &= \frac{ \int_{-L}^{L} \exp\left( -\frac{10}{\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \cdot u \, \mathrm{d}u }{ \int_{-L}^{L} \exp\left( -\frac{10}{\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \mathrm{d}u } \\ &= \frac{ \int_{-L}^{L} \frac{\sqrt{20}}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{20}{2\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \cdot u \, \mathrm{d}u }{ \frac{\sqrt{20}}{\sqrt{2\pi\sigma^2}} \int_{-L}^{L} \exp\left( -\frac{20}{2\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \mathrm{d}u } \\\end{split} \]
このまま L を $$ \infty $$ に近づけると次のようになります。
\[ E = \frac{ \int_{-\infty}^{\infty} \frac{\sqrt{20}}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{20}{2\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \cdot u \, \mathrm{d}u }{ \frac{\sqrt{20}}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^{\infty} \exp\left( -\frac{20}{2\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \mathrm{d}u } \\\]
ここで分子は正規分布の期待値なので、簡単に求められます。
\[ \int_{-\infty}^{\infty} \frac{\sqrt{20}}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{20}{2\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \cdot u \, \mathrm{d}u = \frac{3a_0+4a_1+3a_2}{20}\]
また、分母はガウス関数の積分公式より次のようになります。
\[ \int_{-\infty}^{\infty} \exp\left( -\frac{20}{2\sigma^2} \left(u – \frac{3a_0+4a_1+3a_2}{20} \right)^2 \right) \mathrm{d}u = \frac{\sqrt{2\pi\sigma^2}}{\sqrt{20}}\]
従って、これらを代入すると
\[ E = \frac{3a_0+4a_1+3a_2}{20} \]
となります。
計算結果の考察
1拍の長さを 2u と仮定しましたので、求める1拍の長さの期待値はこの2倍となります。
\[ 2E = \frac{3a_0+4a_1+3a_2}{10} \]
これは、1拍目と2拍目の間隔と、2拍目と3拍目の間隔と、3拍目と4拍目の間隔を、3:4:3で混合した値となっていることがわかります。
Nの値が一般の場合
Nの値が一般の場合は、同様に計算すると、次のようになります。
\[ 2E = \frac{6}{N(N+1)(N+2)} \times \sum_{i=0}^{N} (2i-N)T_i \]
\[ \mathrm{BPM} = \frac{60000}{2E} \]
または、同値ですが、次のように表すこともできます。
\[ 2E = \frac{6}{N(N+1)(N+2)} \times \sum_{i=0}^{N-1} (N-i)(i+1)a_i \]
$$ a_i $$ の係数の具体的な値は次のようになります。
| i=0 | i=1 | i=2 | i=3 | i=4 | i=5 | |
|---|---|---|---|---|---|---|
| N=1 | 1 | |||||
| N=2 | 2 | 2 | ||||
| N=3 | 3 | 4 | 3 | |||
| N=4 | 4 | 6 | 6 | 4 | ||
| N=5 | 5 | 8 | 9 | 8 | 5 | |
| N=6 | 6 | 10 | 12 | 12 | 10 | 6 |
完成品
できたものはこちらに置いてあります。
[数学] ベイズBPM計測器を公開しました | yuinore.net https://t.co/81EDvpWgik
記事を投稿しました。
— ゆいのあ (@yuinore) 2017年10月16日
明日は y_e_af さんで、「関数環P(X), R(X), A(X)について」です。お楽しみに。
![[確率・統計] 中心極限定理：6面サイコロをn回振ったときの、出た目の和の確率分布](https://yuinore.net/wp-content/themes/customizr/assets/front/img/thumb-standard-empty.png)
