y = √x は極値を持つか？

最小値であれば（広義の）極小値である

実数値を取る関数 \( X \to \mathbb{R} \) について、「最小値（最小点）であれば極小値（極小点）である」が成立する。同様に「最大値（最大点）であれば極大値（極大点）である」も成立する。（ただしここでは広義の極大点、極小点を指すものとする。）

1変数関数の局所最適解（極大値・極小値）| 関数の最適化 | 微分積分 | 数学 | ワイズ
https://wiis.info/math/calculus/optimization/maximal-and-minimal-values-of-function/

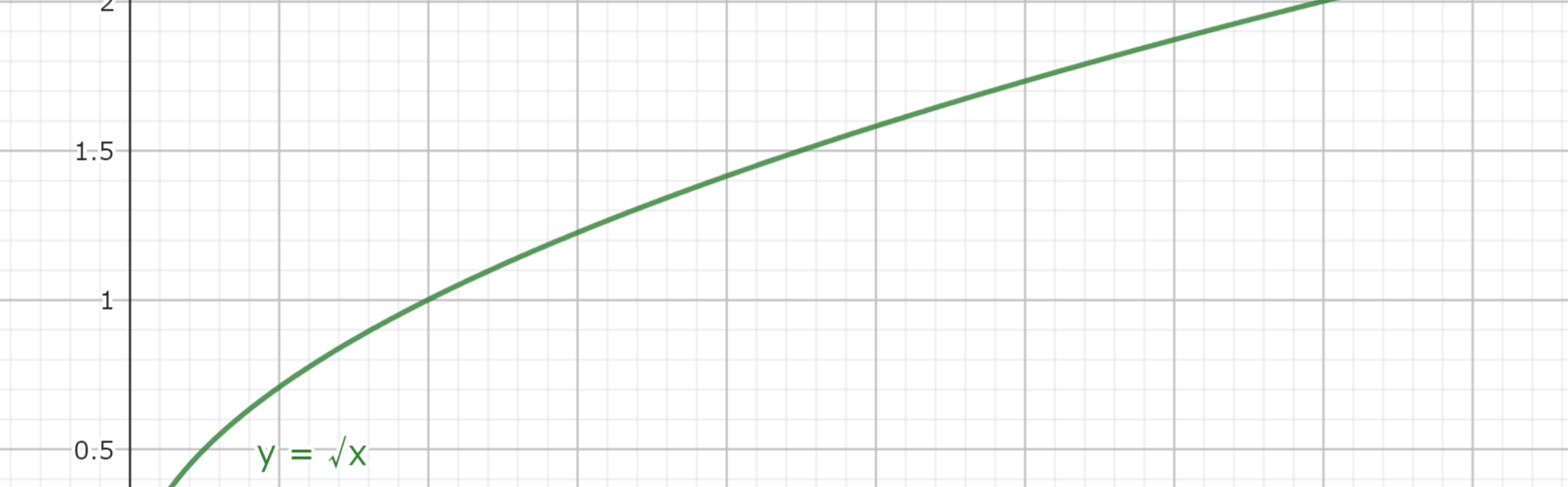
このため、0≦x<∞ で定義された関数 y=√x は x=0 で極小値 0 を持つ。

高校の範囲ではそうではないらしい

しかし、高校の範囲では実数全体で定義された関数についてしか考えられておらず、教科書によっては次のように定義されているらしい。（責め立てるようで申し訳ないのでソースは貼らないでおく。）

f'(x) の符号がある点 x=a の前後で負から正に変化するとき、極小値を取る。
f'(x) の符号がある点 x=a の前後で正から負に変化するとき、極大値を取る。

この定義だと \( f'(x)=\frac{1}{2√x} \) に対して f'(0) が定義されないため、また x<0 では f(x) の定義域から外れるため、極値を取らないというように理解してしまう場合もあるかもしれない。

また、f(x) が減少から増加に転じるときに極小値をとる、というような定義だとしても同様のことが言える。

狭義の極大値・極小値

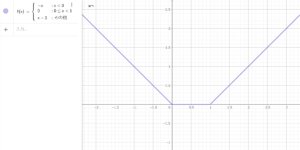
なお、狭義の極値を考える場合は、最小点を持つ場合でも狭義の極小点を持たない場合があるようだ。そのような例として以下の画像のような関数が挙げられる。この場合、最小点は区間 \( [0,1] \) に含まれる任意の点であり、最小値は 0 である。

同様に最大点を持つ場合でも狭義の極大点を持たない場合がある。

多様体として見た場合

一応、より一般の議論として、f(x) を多様体上の関数として見たときにこれが正しいかどうか確認してみる。ここで、定義域 [0,∞) の位相として相対位相を入れておく。また、ここでは狭義の極小点であることを確認する。

証明

f(x)=√x は x=0 で f(x)=0 を取る。このとき、点 0 の開近傍として \( U=[0,1) \) を取ると、すべての \( p \in U \setminus \{0\} \) で \( f(0) \lt f(p) \) となる。
したがって、 f(x) は x=0 で極小値 0 を取る。

多様体M上の関数fの極大値・極小値の定義を教えてください。また、そ… – Yahoo!知恵袋
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13193771833

結論

よって、0≦x<∞ で定義された関数 y=√x は x=0 で狭義の極小値 0 を持つことが分かった。（従って、当然広義の極小値でもある。）

ソースが知恵袋なのでちょっと怪しいですが多分合ってると思います。

おことわり

全部ソースがネットの記事なので間違っていたらごめんなさい。部屋が狭いけど多様体論の教科書が欲しい……。