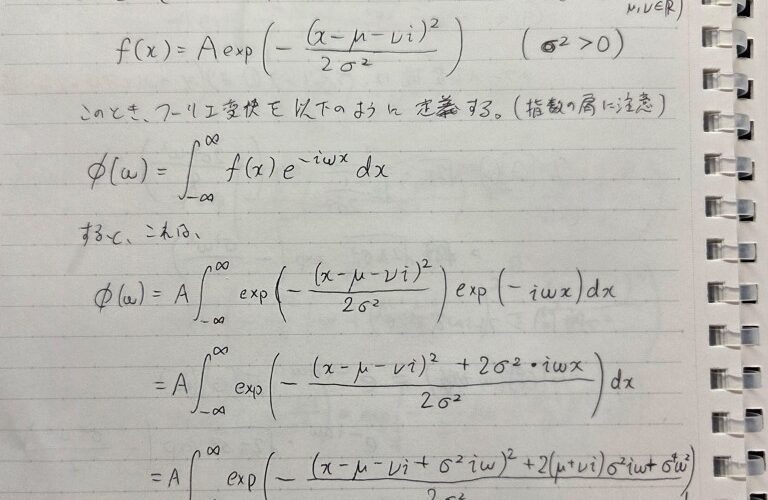問題提起
ガウス関数のフーリエ変換がガウス関数になると言った場合、原点対称のガウス関数
$$
f(x) = A \exp\! \left( – \frac{x^2}{2\sigma^2} \right)
$$
のフーリエ変換が再びその形になることを示しただけで証明が終わりになっていることがある。
しかし、ガウス関数の定義を原点対称とせず、
$$
f(x) = A \exp\! \left( – \frac{(x-\mu)^2}{2\sigma^2} \right)
$$
というように定義する場合、その説明だけでは不十分で、また、このフーリエ変換は実数関数にならない。これは非常に満足度が低い。
代わりに、複素平均をもつガウス関数
$$
f(x) = A \exp\!\left(
-\frac{(x \,-\, \mu_{\mathrm{complex}})^2}{2\sigma^2}
\right)
$$
のフーリエ変換が、再び複素平均をもつガウス関数になることを、実際に手計算で示し、A の範囲についても確認する。
定義の確認
複素期待値を次のように実部と虚部に分けて表記する。(※ 一般的に用いられる表記ではない)
$$
\mu_{\mathrm{complex}} = \mu + \nu i
$$
このとき、回転因子付きガウス関数を次のように定義する。(※ 一般的に呼ばれている名称ではない)
$$
f(x) = A \exp\!\left(
-\frac{(x \,-\, \mu \,-\, \nu i)^2}{2\sigma^2}
\right)
$$
ただし、分散は 0 でないものとし、
$$
\sigma^2 > 0,\; A \in \mathbb{C},\; \sigma \in \mathbb{R},\; \mu,\nu \in \mathbb{R}
$$
とする。
被積分関数の意味について
ここで、この関数 $f(x)$ は、
$$
A=\frac{1}{\sqrt{2\pi\sigma^2}}
$$
とすると、正規分布の確率密度関数の式に対して、平均を $\mu$ ではなく $\mu + \nu i$ とした形である。このため、複素期待値正規分布とも解釈できるが、このとき $f(x)$ は必ずしも実数ではなく、確率分布にはならないことには注意する必要がある。
また、別の言い方をすると、ガウス関数を $\nu i$ だけ平行移動して、定数項 $\in\mathbb{C}$ を掛けた関数でもある。
これが、定数項と回転因子 $e^{i\lambda x}$ と実ガウス関数の積の形に変形できることの確認は読者への課題とする。
フーリエ変換の計算
フーリエ変換の定義(指数の肩の符号に注意)
$$
\phi(\omega) = \int_{-\infty}^{\infty} f(x)\, e^{-i\omega x}\, \mathrm{d}x
$$
を用いて計算すると、
$$
\begin{align}
\phi(\omega)
&= A \int_{-\infty}^{\infty}
\exp\!\left(
-\frac{(x-\mu-\nu i)^2}{2\sigma^2}
\right)
\exp(-i\omega x)\, \mathrm{d}x \\[18pt]
&= A \int_{-\infty}^{\infty}
\exp\!\left(
-\frac{(x-\mu-\nu i)^2 + 2\sigma^2 i\omega x}{2\sigma^2}
\right)\, \mathrm{d}x \\[18pt]
&= A \int_{-\infty}^{\infty}
\exp\!\left(
-\frac{(x-\mu-\nu i + \sigma^2 i\omega)^2
+ 2(\mu+\nu i)\sigma^2 i\omega + \sigma^4\omega^2}
{2\sigma^2}
\right)\, \mathrm{d}x \\[18pt]
&= A \int_{-\infty}^{\infty}
\exp\!\left(
-\frac{(x-\mu-\nu i + \sigma^2 i\omega)^2}{2\sigma^2}
-(\mu+\nu i)i\omega
-\frac{\sigma^2\omega^2}{2}
\right)\, \mathrm{d}x \\[18pt]
&= A
\exp\!\left(
-(\mu+\nu i)i\omega
-\frac{\sigma^2\omega^2}{2}
\right)
\int_{-\infty}^{\infty}
\exp\!\left(
-\frac{(x-\mu-\nu i + \sigma^2 i\omega)^2}{2\sigma^2}
\right)\, \mathrm{d}x \\[18pt]
\end{align}
$$
となる。
ガウス積分に似た箇所の計算
ここで、残った定積分について、参考リンク [1] よりこれを参考にして、(R の定義と積分経路はリンク先を参照のこと)
(i) 1 つ目の積分区間について
$$
x \,-\, \nu i + \sigma^2 i\omega = -R + yi
$$
とおくと、
$$
\mathrm{d}x = i\,\mathrm{d}y
$$
$$
\begin{array}{c|c c c}
x & -R & \longrightarrow & -R + \nu i \,-\, \sigma^2 i\omega \\
\hline
y & -\nu + \sigma^2\omega & \longrightarrow & 0
\end{array}
$$
(ii) 2 つ目の積分区間について
$x \,-\, \nu i + \sigma^2 i\omega$ を $x$ に置き換えて、-R から R まで積分する。
(iii) 3 つ目の積分区間について
$$
x \,-\, \nu i + \sigma^2 i\omega = +R + yi
$$
とおくと、
$$
\mathrm{d}x = i\,\mathrm{d}y
$$
$$
\begin{array}{c|c c c}
x & +R + \nu i \,-\, \sigma^2 i\omega & \longrightarrow & +R \\
\hline
y & 0 & \longrightarrow & -\nu + \sigma^2\omega
\end{array}
$$
以上の経路で積分すると、
$$
\begin{align}
&
\int_{-\infty}^{\infty}
\exp\!\left(
-\frac{(x-\mu-\nu i+\sigma^2 i\omega)^2}{2\sigma^2}
\right)\,\mathrm{d}x
\\[18pt]
=&
\int_{-\infty}^{\infty}
\exp\!\left(
-\frac{(x-\nu i+\sigma^2 i\omega)^2}{2\sigma^2}
\right)\,\mathrm{d}x
\\[18pt]
=&
\lim_{R\to\infty}
\int_{-R}^{R}
\exp\!\left(
-\frac{(x-\nu i+\sigma^2 i\omega)^2}{2\sigma^2}
\right)\,\mathrm{d}x
\\[18pt]
=&
\lim_{R\to\infty}
\Biggl\{
\int_{-\nu+\sigma^2\omega}^{0}
\exp\!\left(
-\frac{(-R+yi)^2}{2\sigma^2}
\right) i\,\mathrm{d}y
\\[6pt]
&\qquad
+ \int_{-R}^{R}
\exp\!\left(
-\frac{x^2}{2\sigma^2}
\right)\,\mathrm{d}x
\\[6pt]
&\qquad
+ \int_{0}^{-\nu+\sigma^2\omega}
\exp\!\left(
-\frac{(+R+yi)^2}{2\sigma^2}
\right) i\,\mathrm{d}y
\Biggr\}
\\[18pt]
=&
\lim_{R\to\infty}
\int_{-R}^{R}
\exp\!\left(
-\frac{x^2}{2\sigma^2}
\right)\,\mathrm{d}x
\\[18pt]
=&
\int_{-\infty}^{\infty}
\exp\!\left(
-\frac{x^2}{2\sigma^2}
\right)\,\mathrm{d}x
\\[18pt]
=&
\sqrt{2\pi\sigma^2}
\end{align}
$$
(ガウス積分)
ガウス積分の結果の代入
よって、元の式に代入すると、
$$
\begin{align}
\phi(\omega)
&= A \sqrt{2\pi\sigma^2} \,
\exp\!\left(
-(\mu+\nu i)i\omega \,-\, \frac{\sigma^2 \omega^2}{2}
\right)
\\[12pt]
&= A \sqrt{2\pi\sigma^2} \,
\exp\!\left(
-\frac{\sigma^2}{2}
\left(
\omega + \frac{\mu+\nu i}{\sigma^2} i
\right)^2
\,-\, \frac{(\mu+\nu i)^2}{2\sigma^2}
\right)
\\[12pt]
&= A \sqrt{2\pi\sigma^2} \,
\exp\!\left(
– \frac{(\mu+\nu i)^2}{2\sigma^2}
\right)
\exp\!\left(
-\frac{\sigma^2}{2}
\left(
\omega + \frac{\mu+\nu i}{\sigma^2} i
\right)^2
\right)
\end{align}
$$
これは再び
$$
\alpha \, \exp\!\left(
-\frac{(x-\beta)^2}{2\gamma^2}
\right)
\qquad
(\alpha \in \mathbb{C} ,\; \gamma^2 > 0 ,\; \beta \in \mathbb{C})
$$
という関数の形になっている。これは満足度が高い。
(ただし $\alpha,\;\beta,\;\gamma$ は定数で、$\omega$ を含まない)
つまり、係数 A を複素数と定義すると、回転因子を持つガウス関数のフーリエ変換が、再び回転因子を持つガウス関数になるということが分かる。一方で、係数 A を実数と定義すると、そのフーリエ変換は、もとの関数集合に含まれず、それの変換が再びそれになるとは言えない。
参考のため、 $f(x)$ に対して特性関数
$$
\varphi(\omega) = \int_{-\infty}^{\infty} f(x)\, e^{i\omega x}\, \mathrm{d}x
$$
を計算した結果も併記しておく。(指数の肩の符号に注意)
$$
\begin{array}{c|c|c|c}
& \text{振幅} & \text{平均} & \text{分散} \\ \hline
\text{フーリエ変換前}
& A
& \mu + \nu i
& \sigma^2
\\ \hline
\text{フーリエ変換後}
& A \sqrt{2\pi\sigma^2} \,
\exp\!\left(
-\dfrac{(\mu+\nu i)^2}{2\sigma^2}
\right)
& -\dfrac{\mu+\nu i}{\sigma^2} i
& \dfrac{1}{\sigma^2}
\\ \hline
\text{特性関数}
& A \sqrt{2\pi\sigma^2} \,
\exp\!\left(
-\dfrac{(\mu+\nu i)^2}{2\sigma^2}
\right)
& +\dfrac{\mu+\nu i}{\sigma^2} i
& \dfrac{1}{\sigma^2}
\end{array}
$$
回転因子とガウス関数型振幅への分解
ここで、以下のように式変形を行うと、これは、回転因子が付いたガウス関数になっていることがわかる。
$$
\begin{align}
\phi(\omega)
&= A \sqrt{2\pi\sigma^2} \,
\exp\!\left(
-\mu i \omega + \nu \omega \,-\, \frac{\sigma^2 \omega^2}{2}
\right)
\\[12pt]
&= A \sqrt{2\pi\sigma^2} \,
\exp\!\left(
-\frac{\sigma^2}{2}
\left(
\omega \,-\, \frac{\nu}{\sigma^2}
\right)^2
+ \frac{\nu^2}{2\sigma^2}
\,-\, \mu i \omega
\right)
\\[12pt]
&=
\underbrace{
A \sqrt{2\pi\sigma^2}\,
e^{\frac{\nu^2}{2\sigma^2}}
}_{\text{定数}}
\cdot
\underbrace{
e^{-\mu i \omega}
}_{\text{回転因子}}
\cdot
\underbrace{
\exp\!\left(
-\frac{\sigma^2}{2}
\left(
\omega \,-\, \frac{\nu}{\sigma^2}
\right)^2
\right)
}_{\text{ガウス型振幅}}
\end{align}
$$
フーリエ変換の変換公式を用いた計算
これは、フーリエ変換の時間シフト公式、および線形性の公式を使うことでも簡単に計算できる。これは読者への課題としたい。
参考リンク一覧
[1] ガウス関数のフーリエ変換|コーシーの積分定理から計算する – あーるえぬ https://math-note.xyz/calculus/fourier-transform-for-gaussian/
[2] 正規分布 – Wikipedia